Записывая очевидное равенство: 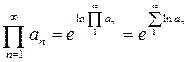 , приходим к выводу о том, что
, приходим к выводу о том, что 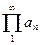 и
и 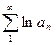 сходятся и расходятся одновременно
сходятся и расходятся одновременно 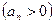 .
.
Def: Бесконечное произведение 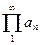 называется сходящимся абсолютно или условно, если абсолютно или условно, соответственно, сходится ряд
называется сходящимся абсолютно или условно, если абсолютно или условно, соответственно, сходится ряд 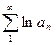 .
.
Примеры:
1°. Рассмотрим 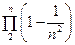 . Для его частичных произведений, получим:
. Для его частичных произведений, получим:
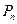 =
= 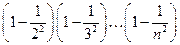 =
= 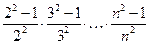 =
=
= 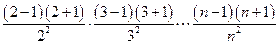 =
= 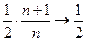 .
.
Бесконечное произведение сходится, по определению.
2°. Рассмотрим 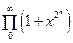 . Для его частичных произведений, получим:
. Для его частичных произведений, получим:
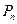 =
= 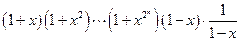 =
= 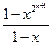 .
.
Произведение сходится, если 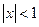 . При этом
. При этом 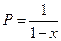 .
.
§. Разложение sin x и cos x в бесконечное произведение.
Запишем формулу Муавра 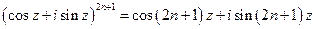 и возьмём мнимую часть от правой и левой части равенства:
и возьмём мнимую часть от правой и левой части равенства:
 =
= 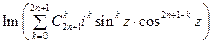 = …
= …
Отметим что при четных 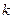 слагаемые в сумме вещественны и, следовательно, нас не интересуют, а при нечетных
слагаемые в сумме вещественны и, следовательно, нас не интересуют, а при нечетных 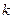 слагаемые чисто мнимые и, поэтому, положив
слагаемые чисто мнимые и, поэтому, положив 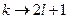 , продолжим выкладку: … =
, продолжим выкладку: … = 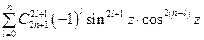 =
=
= 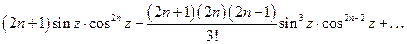 =
= 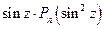 .
.
т.е. 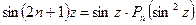 .
.
Разложив 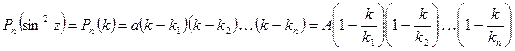 , где
, где 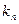 –корни полинома
–корни полинома 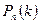 , и отметив что, если
, и отметив что, если 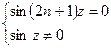 , то z -корень
, то z -корень 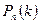 Þ
Þ 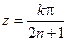 , k = 1,2,…, n. Константа
, k = 1,2,…, n. Константа 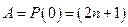 . Учитывая, что
. Учитывая, что 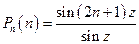 делаем заключение:
делаем заключение: 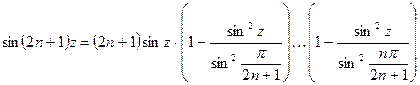 .
.
Положим 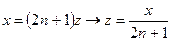 и тогда, при фиксированном k:
и тогда, при фиксированном k:
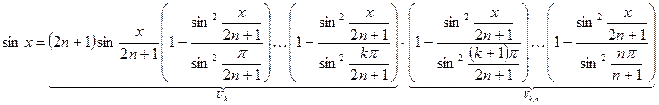
Тогда:
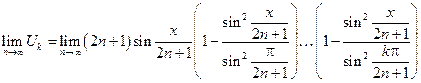 =
= 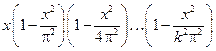 .
.
Чтобы рассмотреть 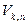 вспомним неравенство
вспомним неравенство 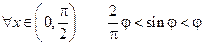 .
.
Тогда: 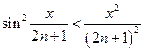 и
и 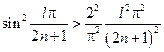 .
.
Следовательно: 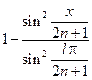
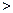
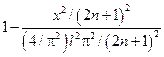 =
= 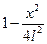 .
.
Таким образом: 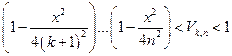 (*)
(*)
Бесконечное произведение 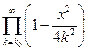 сходится, ибо сходится ряд
сходится, ибо сходится ряд 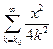 . (Здесь
. (Здесь 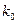 выбрано так, чтобы
выбрано так, чтобы 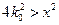 ). Поэтому остаточное произведение
). Поэтому остаточное произведение 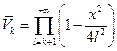 должно стремиться к единице при
должно стремиться к единице при 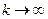 . Очевидно, мы лишь усилим неравенство (*), если напишем:
. Очевидно, мы лишь усилим неравенство (*), если напишем: 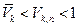 .
.
Переходя к пределу при 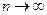 и при фиксированном
и при фиксированном 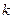 , получаем:
, получаем: 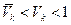 . И, следовательно,
. И, следовательно, 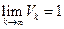 . Мы приходим к разложению
. Мы приходим к разложению 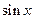 в бесконечное произведение, впервые полученное Эйлером:
в бесконечное произведение, впервые полученное Эйлером: 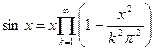 .
.
Учитывая, что 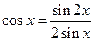 и используя полученное разложение
и используя полученное разложение 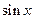 в бесконечное произведение, можем получить разложение
в бесконечное произведение, можем получить разложение 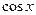 в бесконечное произведение.
в бесконечное произведение.
В самом деле:
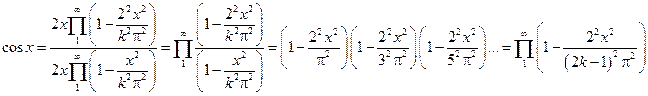 .
.
Тоже самое разложение можно получить и записав 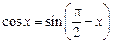
 , а положив в разложении
, а положив в разложении 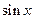 ,
, 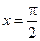 получим формулу Валлиса:
получим формулу Валлиса: 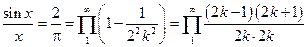 =
=
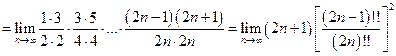 .
.
 2015-06-24
2015-06-24 1807
1807








