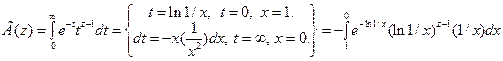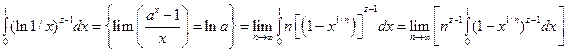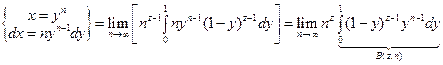2015-06-24
585
=
= 
=
= 
.
Функция В (z, n) – называется Бетта-функцией.
§. БеТта – функциЯ В(а,b)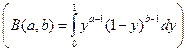 
.
Изучим свойства введенной функции:
а )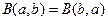 
.
Δ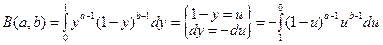 
= 
. ▲
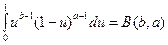б).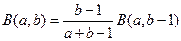 
.
=
= 
=
= 
=
= 
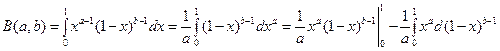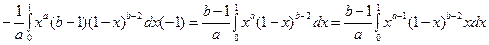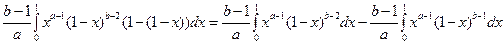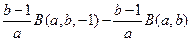. Отсюда получается доказываемая формула.
Итак, имеем: 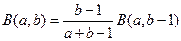и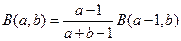 
.
Если b – целое число, то: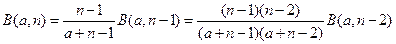 
= … =
= 
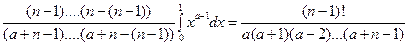Þ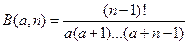 
.
Если, при этом, а – также целое, то: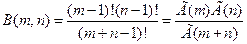 
.
Эта формула полученная для целочисленных значениях аргументов справедлива и в общем случае: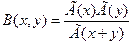 
.
в). Еще одно выражение для Бета-функции:
=
= 
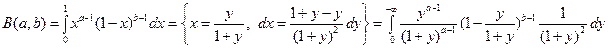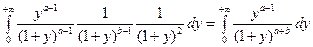. Т.е. 
.
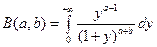Кстати, при b = 1 – a: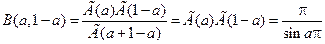 
.
ЕЩЕ РАЗ Гамма – функция Г(z).
Возвращаемся к Гамма-функции. Нами установлено:
.
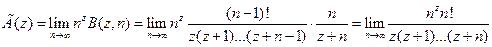Последняя выкладка показывает, что функция, введенная в п.7, как эйлеровый интеграл 2-го рода, действительно совпадает с Гамма-функцией, определенной в начале раздела.
