Общие сведения. Раздел 6. Бесконечные произведения

РАЗДЕЛ 6. Бесконечные произведения.

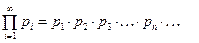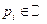Def: Конструкция вида , где (или 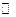) называется бесконечным произведением. При этом, 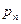– общий член произведения, а

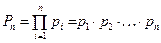– частичные произведения.

Def: Если 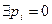, то бесконечное произведение называется “нулевым бесконечным произведением”.

Def: Есл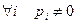и 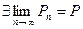и и 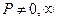, то бесконечное произведение называется сходящимся к P.

Def: Есл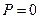и и 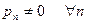то произведение называется расходящимся к нулю.

Рассмотрим 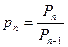и перейдём к пределу при 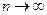. Если произведение сходится то:

.

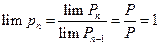Получили: необходимое условие сходимости бесконечного произведения:

*. Если бесконечное произведение сходится, то его общий член стремится к единице.

Примеры:

1°. 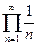. Частичные произведения 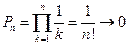, однако при этом 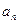не стремится к единице. Не выполнено необходимое условие сходимости бесконечного произведения, хотя 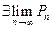. Этот пример поясняет термин: «произведение расходится к нулю».

2°. 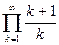. Казалось бы: 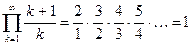, но

.

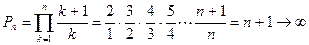Бесконечное произведение расходится, хотя 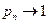при 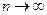, т.е. стремление к единице общего члена произведения, есть только необходимое, но не достаточное условие сходимости.

*. Каждому бесконечному произведению 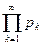можно поставить в соответствие последовательность его частичных произведений 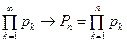и, наоборот:

.

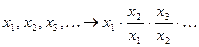Причём последовательность и произведение сходятся или расходятся одновременно (по определению), за исключением произведений расходящихся к нулю.