Запишем разложения: 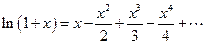 и
и 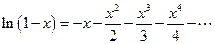 , а после этого, вычтем из первого разложения второго:
, а после этого, вычтем из первого разложения второго:
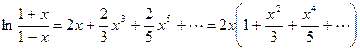 .
.
Положим в этой формуле 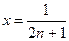 . Тогда:
. Тогда: 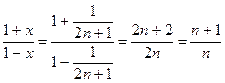 и, следовательно:
и, следовательно:
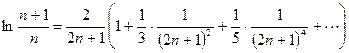 Þ
Þ
Þ 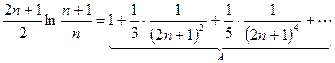 . И, очевидно,
. И, очевидно, 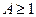 .
.
Оценка сверху для 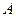 дает следующее:
дает следующее: 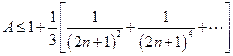 =
= 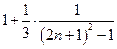 =
=
= 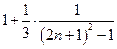 =
= 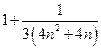 =
= 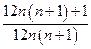 =
= 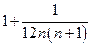 .
.
Из оценок для 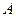 , получаем:
, получаем: 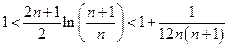 и, потенцируя:
и, потенцируя:
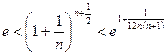 . (*)
. (*)
Теперь рассмотрим последовательность: 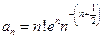 .
.

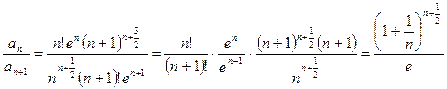 .
.
учитывая (*), получаем: 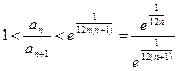 .
.
Таким образом: 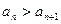 и
и 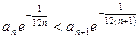 .
.
Последовательность 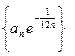 возрастающая и ограничена сверху
возрастающая и ограничена сверху 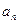 . Значит
. Значит 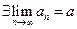 и
и
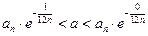 Þ
Þ 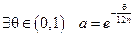 Þ
Þ 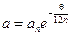 , т.е.
, т.е. 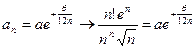 Þ
Þ
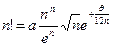 .
.
Для нахождения величины a воспользуемся формулой Валлиса:
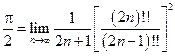 .
.
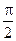 =
= 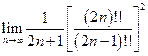 =
= 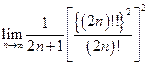 =
= 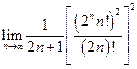 = ….
= ….
Подставляя вместо 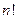 , полученное для него выражение, получаем
, полученное для него выражение, получаем 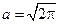 .
.
Тогда: 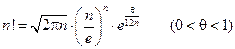 . Это и есть формула Стирлинга.
. Это и есть формула Стирлинга.
РАЗДЕЛ 7. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ.
 2015-06-24
2015-06-24 1209
1209








