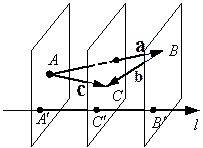2015-06-24
3785
Определение. Проекцией точки 
на ось 
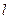называется точка 
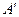- точка пересечения этой оси с плоскостью, проходящей через точку 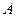, перпендикулярно оси 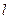(рис. 2.17).
Определение. Геометрической проекцией вектора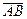 
на ось 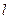называется вектор 
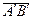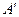, где и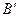 
соответственно проекции
Рис. 2.17 точек 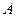и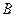 
на ось .
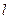Пусть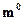 
орт направления оси 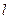, тогда существует такое число 
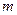, что вектор 
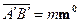. Число 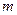называют алгебраической проекцией вектора 
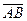на ось 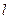и обозначают пр 
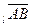или пр 
.
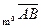Очевидно, пр =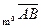 
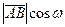, где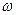 
- угол между вектором 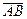и положительным направлением оси .
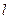Имеют место следующие свойства:
а)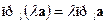 
;
б)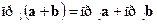 
.
Рассматривая отдельно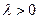 
и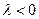 
легко установить свойство а). Второе свойство очевидно.
Определение. Проекцией точки 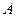на плоскость 
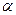называется точка 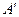- точка пересечения этой плоскости и перпендикуляра, опущенного из точки 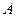на плоскость (рис. 2.18).
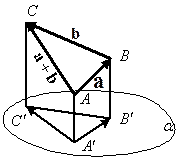Определение. Проекцией вектора 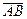на плоскость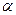
называют вектор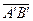 
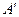, где и 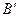проекции точек 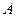и 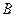на эту плоскость и обозначают её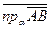 
Рис. 2.18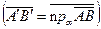 
.
Свойства проекции вектора на плоскость:
а)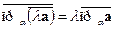 
(постоянный множитель можно выносить за знак проекции);
|
|
|
б)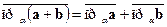 
(проекция суммы равна сумме проекций).
Справедливость свойства усматривается из рисунка 2.18.
