Определение. Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов и косинуса угла между ними.
Скалярное произведение векторов 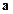 и
и  обозначается
обозначается 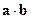 (или
(или 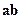 , или
, или 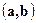 ).
).
Если 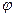 - угол между векторами
- угол между векторами 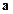 и
и  , то по определению
, то по определению 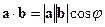 .
.
Так как 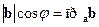 , то справедлива формула
, то справедлива формула 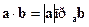 . Справедлива и формула
. Справедлива и формула 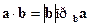 .
.
Итак, 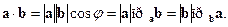
Скалярное произведение двух векторов равно произведению длины одного из этих векторов и проекции другого на направление первого.
Скалярное произведение векторов обладает следующими свойствами.
1). 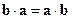 (коммутативный закон). Это свойство непосредственно следует из определения скалярного произведения.
(коммутативный закон). Это свойство непосредственно следует из определения скалярного произведения.
2). 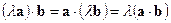 (ассоциативный закон). ►Действительно,
(ассоциативный закон). ►Действительно, 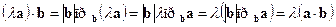 .◄
.◄
3). 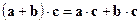 (дистрибутивный закон.) ►
(дистрибутивный закон.) ► 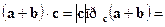
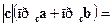
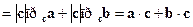 ◄
◄
4). 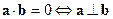 .
.
Скалярное произведение векторов 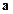 и
и  равно нулю тогда и только тогда, когда векторы
равно нулю тогда и только тогда, когда векторы 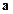 и
и  перпендикулярны.
перпендикулярны.
►Необходимость. Пусть 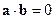 , тогда
, тогда 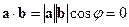 , откуда либо один из векторов нулевой, либо
, откуда либо один из векторов нулевой, либо 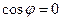 . Если один из векторов нулевой, то ему можно приписать любое направление, и векторы
. Если один из векторов нулевой, то ему можно приписать любое направление, и векторы 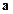 и
и  перпендикулярны. Если же
перпендикулярны. Если же 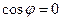 , то угол
, то угол 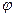 прямой и векторы
прямой и векторы 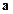 и
и  перпендикулярны.
перпендикулярны.
Доказано, что из 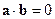 следует
следует 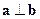 .
.
Достаточность. Пусть 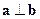 , тогда
, тогда 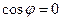 , а, следовательно,
, а, следовательно, 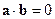 . Следовательно, из
. Следовательно, из 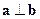 следует
следует 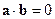 .◄
.◄
5). 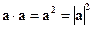 .
.
Скалярный квадрат вектора равен квадрату длины этого вектора.
►Действительно, 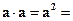
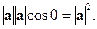 ◄
◄
 2015-06-24
2015-06-24 914
914








