Пусть функциональная последовательность (1) сходится на числовом множестве M к предельной функции 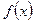 . Это означает, что
. Это означает, что
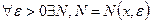 , такое, что при всех
, такое, что при всех 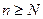 будет
будет 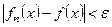 .
.
Обратим внимание на то, что N зависит не только от 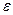 , но и от точки
, но и от точки 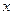 .
.
Если номер 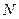 оказывается пригодным сразу для всех значений
оказывается пригодным сразу для всех значений 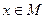 и зависит только от
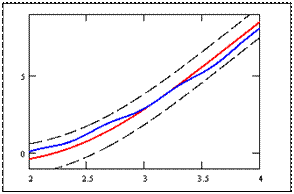
и зависит только от 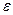 . В этом случае функциональную последовательность (1) называют равномерно сходящейся на множестве M.
. В этом случае функциональную последовательность (1) называют равномерно сходящейся на множестве M.
Пусть на числовом множестве 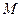 задана функциональная последовательность (1). Говорят, что эта последовательность сходится на множестве M равномерно к функции
задана функциональная последовательность (1). Говорят, что эта последовательность сходится на множестве M равномерно к функции 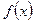 , если выполняется:
, если выполняется:
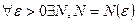 , такое, что при всех
, такое, что при всех 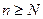 и
и 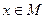 будет
будет 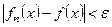 . (6)
. (6)
 2015-06-24
2015-06-24 710
710








