Th 1. Достаточный признак Вейерштрасса для равномерной сходимости функционального ряда

Пусть 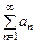(10) – сходящийся числовой ряд с положительными членами, а функциональный ряд (3) таков, что при всех натуральных n и при всех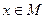

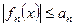(11),

тогда функциональный ряд (3) сходится равномерно на множестве M.

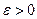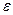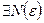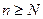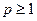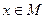□ Возьмем произвольное . Тогда в силу сходимости числового ряда (10) для этого выполняется , такое, что при всех , и будет 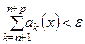. Тогда в силу (11) будет выполняться (9) 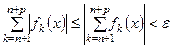. А в силу критерия Коши это означает равномерную сходимость функционального ряда (4).

■

Замечание. Числовой ряд (10) называется мажорирующим рядом для функционального ряда (3).

I Исследуем на равномерную сходимость ряд , .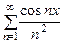

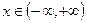Сходящийся знакоположительный числовой ряд 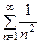является мажорирующим для него, т.к.

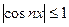
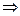
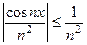. Поэтому исходный функциональный ряд сходится равномерно.