Функциональные последовательности и ряды
Пусть M – некоторое числовое множество
Если каждому натуральному числу n поставлена в соответствие некоторая функция 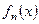 определенная на множестве M, то говорят, что на множестве M задана функциональная последовательность
определенная на множестве M, то говорят, что на множестве M задана функциональная последовательность
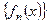 . (1)
. (1)
|
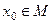 функциональная последовательность (1) превращается в числовую
функциональная последовательность (1) превращается в числовую 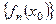 .
. I 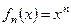 ,
, 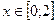
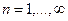 .
.
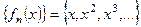 .
.
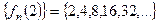 .
.
Пусть на множестве M определена функциональная последовательность и при 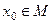 функциональная последовательность (1) превращается в сходящуюся числовую последовательность
функциональная последовательность (1) превращается в сходящуюся числовую последовательность 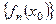 . Тогда говорят, что функциональная последовательность (1) сходится в точке
. Тогда говорят, что функциональная последовательность (1) сходится в точке 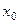 .
.
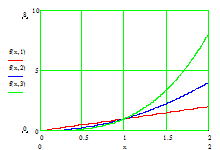
I Функциональная последовательность 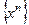 сходится в точках
сходится в точках
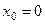
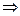
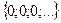 ,
, 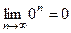 ,
,
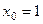
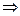
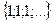 ,
, 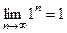 ,
,
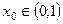
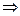
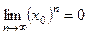 .
.
Если функциональная последовательность сходится в каждой точке множества M, говорят, что она сходится на множестве M.
I Функциональная последовательность 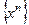 сходится на множестве
сходится на множестве 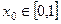
Пусть функциональная последовательность (1) сходится на множестве M и 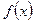 функция, которая на множестве M определяется формулой
функция, которая на множестве M определяется формулой
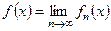 , (2)
, (2)
тогда 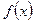 называется предельной функцией функциональной последовательности (1) на множестве M.
называется предельной функцией функциональной последовательности (1) на множестве M.
|
функциональной последовательности
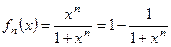 ,
, 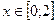 ,
, 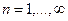 .
.
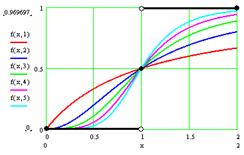
При 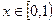
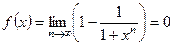 ,
,
При 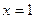
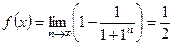 ,
,
При 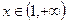
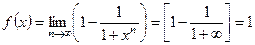 .
.
Таким образом, предельная функция имеет вид 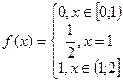 .
.
Пусть на множестве M определена функциональная последовательность 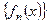 , тогда выражение
, тогда выражение
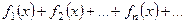
или
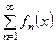 (3)
(3)
называется функциональным рядом на множестве M (функциональный ряд).
При каждом фиксированном 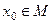 функциональный ряд (3) превращается в числовой ряд.
функциональный ряд (3) превращается в числовой ряд.
Пусть на множестве M задан функциональный ряд 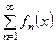 тогда функции
тогда функции
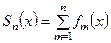 (4)
(4)
называются частичными суммами функционального ряда.
Говорят, что функциональный ряд (3), заданный на множестве M сходится или расходится в точке 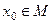 , если в этой точке сходится или расходится функциональная последовательность частичных сумм функционального ряда, т.е. сходится или расходится числовой ряд
, если в этой точке сходится или расходится функциональная последовательность частичных сумм функционального ряда, т.е. сходится или расходится числовой ряд 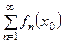 .
.
Пусть функциональный ряд (3) сходится на числовом множестве M и 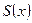 - предельная функция функциональной последовательности частичных сумм функционального ряда (4), тогда эту функцию
- предельная функция функциональной последовательности частичных сумм функционального ряда (4), тогда эту функцию 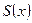 называем суммой данного функционального ряда и пишут
называем суммой данного функционального ряда и пишут
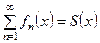 . (5)
. (5)
Очевидно, при каждом 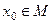
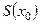 является обычной суммой числового ряда
является обычной суммой числового ряда 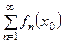 .
.
 2015-06-24
2015-06-24 906
906