Th 3. О дифференцируемости предельной функции

Пусть все функции функциональной последовательности (1) непрерывно-дифференцируемы на отрезке 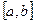(т.е. имеют непрерывную производную), причем функциональная последовательность составленная из производных 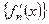(16)

равномерно сходится на этом отрезке. Тогда предельная функция 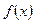дифференцируема на 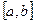, причем выполняется:

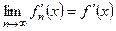. (17)

При этом говорят, что допустим предельный переход под знаком производной.

□

Обозначим 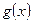- предельную функцию последовательности (16), то есть .

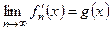В силу теоремы об интегрируемости предельной функции выполняется:

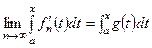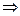
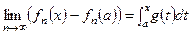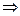
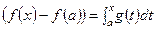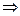, , , дифференцируем 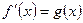. Отсюда следует (17).

■

Рассмотрим теперь функциональный ряд (3) равномерно сходящийся на числовом промежутке M к сумме 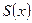переформулировав теоремы 1-3 для предельной функции последовательности 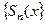частичных сумм ряда (3) автоматически получаем следующие утверждения.