Пусть функциональная последовательность 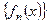 (была (1)) сходится равномерно к предельной функции
(была (1)) сходится равномерно к предельной функции 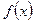 на числовом промежутке M.
на числовом промежутке M.
Th 1. О непрерывности предельной функции.
Пусть все функции функциональной последовательности (1) непрерывны на M, тогда и предельная функция 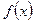 непрерывна на множестве M.
непрерывна на множестве M.
□ Пусть 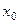 произвольная точка множества M. Возьмем произвольно
произвольная точка множества M. Возьмем произвольно 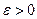 .
.
В силу равномерной сходимости функциональной последовательности (1) найдется N для которого для любого x 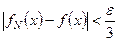 и в частности
и в частности 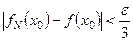 . (12)
. (12)
В силу непрерывности функции 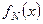 в точке
в точке 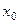 для взятого
для взятого 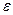 и
и 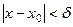 (13)
(13)
выполняется 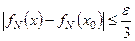 . (14)
. (14)
Тогда при всех x удовлетворяющих (13) в силу (12) и (14) будет выполняться 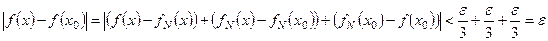 .
.
■
 2015-06-24
2015-06-24 904
904








