Разложение непрерывной функции в ряд Тейлора

Пусть функция 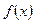определена и непрерывна на числовом промежутке M, 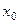- внутренняя точка этого промежутка.

Если существует такая последовательность действительных чисел 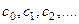, что 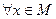выполняется равенство

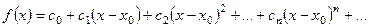(8)

,

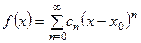то говорят, что функция 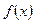в промежутке M разложена в степенной ряд с центром .

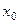В частности, если промежуток M является интервалом, то говорят также о разложении функции 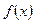в степенной ряд в окрестности точки .

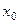Из теоремы о тождестве степенных рядов вытекает, что в случае если функция 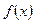может быть разложена в степенной ряд в промежутке M, то разложение будет единственным.

Пусть функция 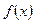имеет в точке 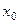производные всех порядков, то есть бесконечно дифференцируема, тогда степенной ряд

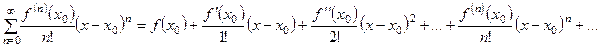(9)

называется рядом Тейлора для функции 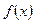с центром 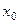или рядом Тейлора для функции 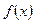в окрестности .

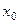Если 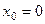, то ряд Тейлора называют рядом Маклорена. Ряд Маклорена имеет вид

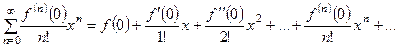(10)