2.1. Скалярное поле и его характеристики:
Определение: все пространство или любая его часть, в каждой точке которой задана некоторая скалярная величина 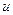 , называется скалярным полем.
, называется скалярным полем.
Характеристики скалярного поля:
1 ) Поверхности уровня: 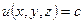 ; линии уровня:
; линии уровня: 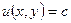 .
.
2) Производная по направлению.
Формула вычисления: 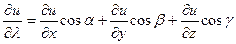 , где
, где 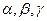 - углы,
- углы,
образованные направлением дифференцирования 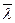 с соответствующими
с соответствующими
координатными осями.
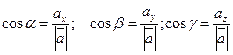
Производная 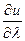 характеризует скорость изменения функции поля в заданном
характеризует скорость изменения функции поля в заданном
направлении.
3) Градиент:
Формула вычисления: 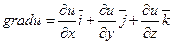 ;
;
Свойства градиета:
- направлен по нормали к поверхности уровня;
- определяет направление, по которому 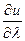 достигает наибольшего значения и, следовательно, функция поля
достигает наибольшего значения и, следовательно, функция поля 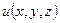 растет быстрее всего.
растет быстрее всего.
2.2. Векторное поле и его характеристики:
Определение:
Все пространство или любая его часть, в каждой точке которой задана некоторая векторная физическая величина 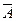 , называется векторным полем.
, называется векторным полем.
Векторное поле считается заданным, если задан вектор 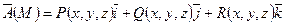 .
.
Характеристики векторного поля
1) Векторные линии:
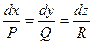 - система дифференциальных уравнений векторных линий;
- система дифференциальных уравнений векторных линий;
2) Поток:
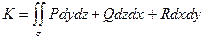
и в частности, 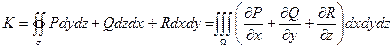 ;
;
В поле скоростей текущей жидкости поток вектора поля через поверхность 
определяет количество жидкости, протекающей через эту поверхность в единицу времени – физический смысл потока через незамкнутую поверхность.
В поле скоростей текущей жидкости поток вектора поля изнутри поверхности 
определяет разность между количеством жидкости вытекающей и втекающей в
область 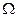 в единицу времени - физический смысл потока через замкнутую поверхность.
в единицу времени - физический смысл потока через замкнутую поверхность.
3) Дивергенция: 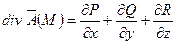 .
.
Если 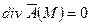 , то поле называется соленоидальным.
, то поле называется соленоидальным.
Физический смысл дивергенции:
В поле скоростей текущей жидкости дивергенция векторного поля в точке 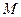 характеризует мощность источника или стока, находящегося в этой точке.
характеризует мощность источника или стока, находящегося в этой точке.
4 ) Циркуляция: 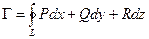 , также по формуле:
, также по формуле:
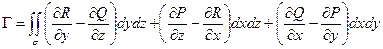 .
.
Физический смысл: циркуляция силового поля вдоль замкнутого контура, помещенного в поле, выражает работу этого поля при перемещении материальной точки вдоль замкнутого контура.
5 )Ротор: 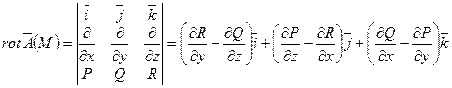 .
.
Физический смысл: в поле скоростей вращающейся жидкости ротор поля с точностью до числового множителя равен угловой скорости.
Если 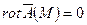 , то поле потенциальное.
, то поле потенциальное.
Потенциал находим по формуле:
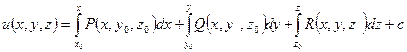 , здесь
, здесь 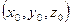 - координаты произвольной фиксированной точки поля,
- координаты произвольной фиксированной точки поля, 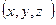 - координаты переменной точки поля.
- координаты переменной точки поля.
Если 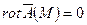 ,
, 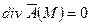 , то поле называется гармоническим.
, то поле называется гармоническим.
 2015-06-26
2015-06-26 367
367







