2015-07-04
1843
Базисный репер. Компоненты векторов.
Введем в трехмерном пространстве репер из трех линейно независимых векторов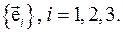 
В общем случае эти вектора являются ни единичными ни ортогональными. Тогда произвольный вектор 
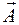может быть представлен в этом репере выражением
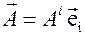
Числа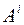 
называются компонентами вектора в базисе 
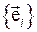и зависят от выбора этого базиса.
Введем величину
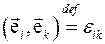
Эта величина является симметричным тензором второго ранга. Матрица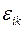 
, представляющая этот тензор, в силу линейной независимости векторов 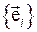является неособенной, т.е. 
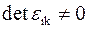и в случае ортогонального и нормированного репера – единичной. Тогда скалярное произведение двух векторов 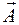и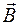 
в нашем пространстве, с учетом выражения (3.1), может быть представлено в виде
,
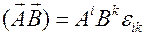Поскольку матрица 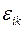неособенная мы можем ввести матрицу 
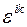такую, что
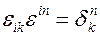
Введем базис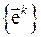 
, дополняющий базис 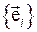. По определению положим
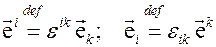(3.5)
Тогда, как легко увидеть,
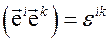, (3.6)
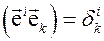. (3.7)
Следовательно, вектора дополняющего и основного базисов ортогональны. Поскольку 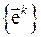также базис, произвольный вектор 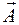может быть разложен по базису 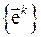и представлен в виде
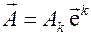, (3.8)
где числа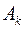 
являются компонентами вектора 
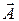в дополняющем базисе 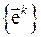. Между числам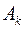и и 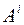нетрудно установить связь:
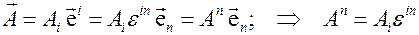, (3.9)
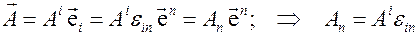. (3.10)
Полученные соотношения (3.9) и (3.10) называются правилами поднятия и опускания индексов.
Теперь выражение для скалярного произведения векторов примет вид
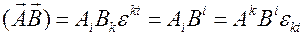. (3.11)
Найдем выражения для компонент вектора 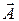в обоих базисах.
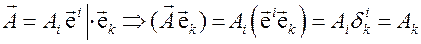, (3.12)
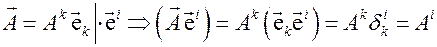(3.13)
Следовательно,
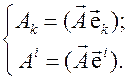(3.14)
Полученные соотношения (3.14) взаимно однозначно ставят в соответствие вектору 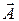его компоненты 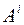в базисе 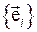или компоненты 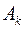в базисе 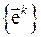. Эти компоненты вектора называются контравариантными и ковариантными соответственно.
Очевидно, что в пространстве существует бесконечное количество базисов. Выберем из всего множества базисов другой базис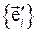 
. Тогда вектора, составляющие этот базис, могут быть представлены в исходном базисе 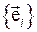следующим образом
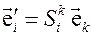, (3.15)
где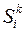 
-матрица, описывающая преобразование базиса 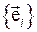в базис 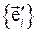(верхний индекс матрицы помечает столбцы, а нижний – строки). Установим связь базиса 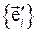с дополняющим базисом 
:
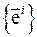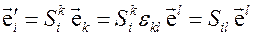, (3.16)
где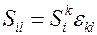 
. Воспользуемся определением (3.2). Тогда получим
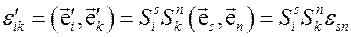(3.17)
Если оба базиса 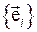и 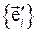ортонормированы, то матрица 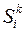ортогональна, поскольку 
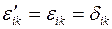. Итак, для основных базисов мы установили закон преобразования (3.15). Найдём закон преобразования для дополняющих базисов. Мы имеем
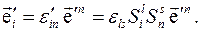
С другой стороны
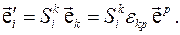
Поэтому
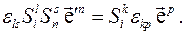
Переобозначим индексы слева
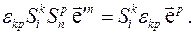
Теперь
;
.
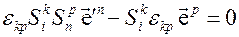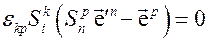Тогда
.
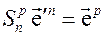Отсюда получаем закон преобразования дополняющего базиса
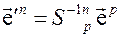. (3.18)
Таким образом, мы установили законы преобразования прямых и дополняющих базисов. Установим законы преобразования компонент вектора 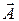при преобразованиях базисов. Для произвольного вектора 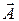получаем:
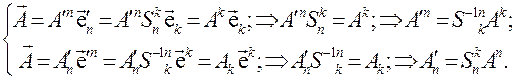(3.19)
Теперь видно, что компоненты вектора в основном базисе (контравариантные компоненты) преобразуются по закону преобразования дополняющего базиса, а компоненты вектора в дополняющем базисе (ковариантные компоненты) преобразуются по закону преобразования основного базиса. Выделим эти законы:
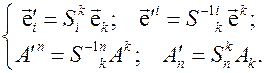(3.20)
Отсюда становятся понятными принятые названия для компонент вектора: ковариантный – преобразующийся, так же как и основной базис, контравариантный – преобразующийся не так как основной базис.
