Рассмотрим еще один пример подвижного репера – репер Френе. Будем полагать, что материальная частица движется по кривой линии (Рис.2), заданной выражением
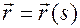
где 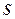 - длина дуги, отсчитываемая по траектории движения частицы. Тогда скорость частицы несложно найти продифференцировав выражение (4.1) по времени
- длина дуги, отсчитываемая по траектории движения частицы. Тогда скорость частицы несложно найти продифференцировав выражение (4.1) по времени
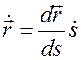
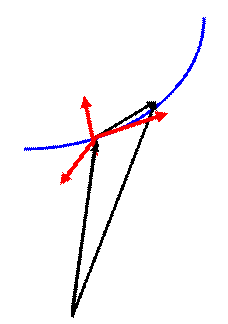
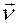
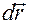
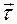
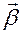
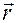
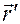
Рис. 1.
Поскольку 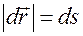 то
то 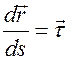 - единичный вектор, направленный по касательной к траектории. Следовательно,
- единичный вектор, направленный по касательной к траектории. Следовательно,
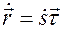 .
.
Найдем ускорение частицы, продифференцировав выражение (4.3) по времени
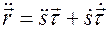 ,
,
где 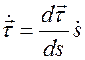 .
. 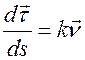 - вектор, направленный по нормали к траектории.
- вектор, направленный по нормали к траектории. 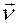 - единичный вектор. Для ускорения частицы мы получаем следующее выражение
- единичный вектор. Для ускорения частицы мы получаем следующее выражение
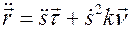
Таким образом, у нас вполне естественно возникли два единичных и ортогональных вектора, составляющих часть подвижного репера. Введем третий орт репера по стандартному правилу
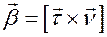
Полученный таким образом репер называется репером Френе 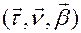 . Этот репер выделяет в пространстве три плоскости:
. Этот репер выделяет в пространстве три плоскости: 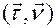 - соприкасающаяся,
- соприкасающаяся, 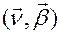 - нормальная и
- нормальная и 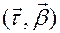 - спрямляющая. Найдем закон изменения орта
- спрямляющая. Найдем закон изменения орта 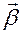 при движении по траектории. Для этого продифференцируем определение
при движении по траектории. Для этого продифференцируем определение 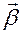 (4.5) по длине дуги
(4.5) по длине дуги
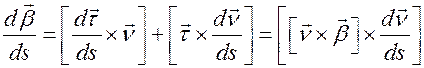 .
.
Воспользуемся известным соотношением
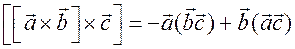 .
.
В нашем случае 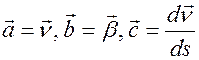 . Следовательно
. Следовательно
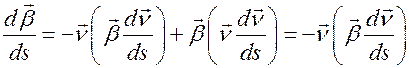 .
.
Введем обозначение 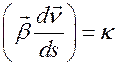 . Тогда получаем закон изменения орта
. Тогда получаем закон изменения орта 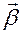 при движении материальной точки по траектории в виде
при движении материальной точки по траектории в виде
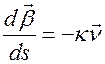
Далее находим закон изменения орта 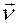 при движении материальной точки по траектории
при движении материальной точки по траектории
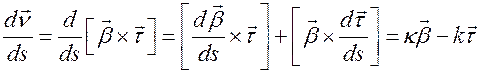 .
.
Таким образом, мы пришли к уравнениям, которые описывают изменение репера Френе при движении материальной частицы по траектории. Эти уравнения называются уравнениями Френе. Выпишем уравнения Френе
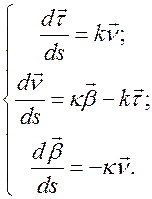
Выясним смысл коэффициентов 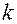 и
и 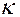 , входящих в уравнения Френе (6.8). Разложим векторную функцию
, входящих в уравнения Френе (6.8). Разложим векторную функцию 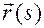 в ряд Тейлора вблизи точки
в ряд Тейлора вблизи точки 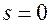 . Используя уравнения Френе (6.8) будем иметь
. Используя уравнения Френе (6.8) будем иметь
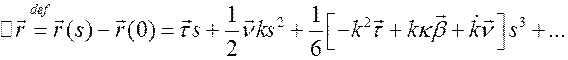
Проектируем вектор 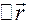 на направления
на направления 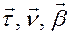 (см. рис. 2)
(см. рис. 2)
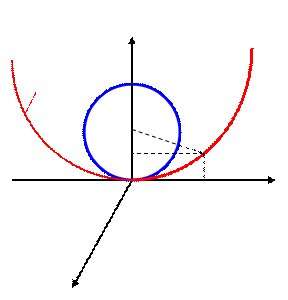
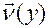
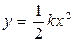

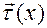
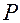
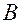
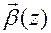
Рис. 2.
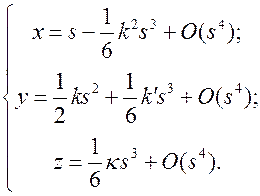
Как несложно увидеть из выражений (6.9), в квадратичном приближении проекцией траектории на соприкасающуюся плоскость является парабола
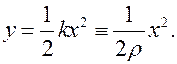
В точке  исследуемая кривая касается оси
исследуемая кривая касается оси  . При сдвиге вдоль кривой на величину
. При сдвиге вдоль кривой на величину 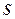 кривая и ось расходятся на расстояние
кривая и ось расходятся на расстояние 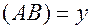 . Если
. Если 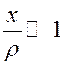 , то
, то 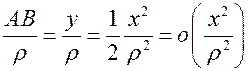 - малая величина второго порядка. Это дает нам основание говорить о касании первого порядка осью
- малая величина второго порядка. Это дает нам основание говорить о касании первого порядка осью 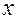 исследуемой кривой в точке
исследуемой кривой в точке 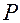 . Проведем окружность радиуса
. Проведем окружность радиуса 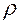 с центром в точке
с центром в точке 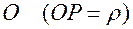 на оси
на оси 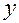 . Окружность касается кривой в точке
. Окружность касается кривой в точке 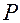 . При сдвигах вдоль кривой кривая и окружность расходятся на расстояние
. При сдвигах вдоль кривой кривая и окружность расходятся на расстояние 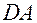 . Вычислим это расстояние
. Вычислим это расстояние
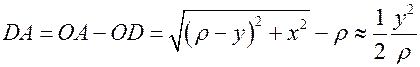 .
.
Поэтому
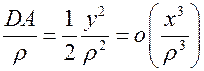 .
.
Таким образом, мы имеем касание второго порядка окружностью кривой в точке 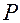 . Поэтому мы можем утверждать, что
. Поэтому мы можем утверждать, что 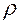 - радиус кривизны кривой, а, соответственно,
- радиус кривизны кривой, а, соответственно, 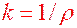 - ее кривизна.
- ее кривизна.
Рассмотрим проекцию кривой на спрямляющую плоскость 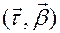 . Из (6.9) нетрудно заметить, что эта проекция имеет вид кубической параболы
. Из (6.9) нетрудно заметить, что эта проекция имеет вид кубической параболы
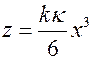 .
.
Эта кривая проходит из нижней полуплоскости в верхнюю (из верхней в нижнюю), если 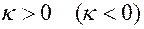 , а рассматриваемая точка
, а рассматриваемая точка 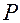 на кривой есть точка перегиба. Это дает нам возможность трактовать
на кривой есть точка перегиба. Это дает нам возможность трактовать 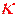 как кручение кривой.
как кручение кривой.
Теорема. Значения кривизны 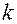 и кручения
и кручения 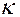 как функции длины дуги однозначно определяют форму кривой, независимо от положения этой кривой в пространстве.
как функции длины дуги однозначно определяют форму кривой, независимо от положения этой кривой в пространстве.
Докажем эту важную теорему. Необходимость доказываемого утверждения очевидна, поскольку если известна кривая, то значения 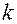 и
и 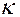 легко восстанавливаются, например, из уравнений Френе.
легко восстанавливаются, например, из уравнений Френе.
Достаточность. Положим, что известны функции 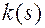 и
и 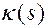 . Рассмотрим уравнения Френе (6.8), в которых векторы
. Рассмотрим уравнения Френе (6.8), в которых векторы 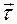 ,
, 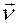 и
и 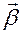 являются искомыми функциями. Докажем следующую лемму: ортонормированность репера Френе в любой точке
являются искомыми функциями. Докажем следующую лемму: ортонормированность репера Френе в любой точке 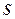 кривой обеспечивается ортонормированностью его в начальной точке.
кривой обеспечивается ортонормированностью его в начальной точке.
Введем обозначения 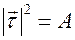 .
. 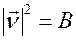 .
. 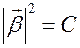 ,
, 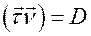 ,
, 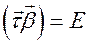 и
и 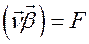 . Используя уравнения Френе (6.8) нетрудно получить уравнения для введенных функций
. Используя уравнения Френе (6.8) нетрудно получить уравнения для введенных функций
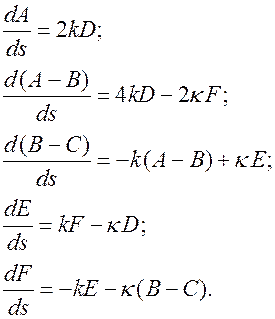
Последние пять уравнений являются замкнутой системой однородных линейных уравнений относительно искомых 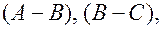
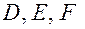 . Единственным решением этой системы, удовлетворяющим начальным условиям
. Единственным решением этой системы, удовлетворяющим начальным условиям
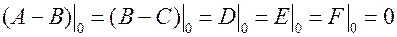 ,
,
является
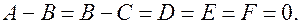
Из первого уравнения следует при данных начальных условиях, что 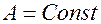 . Если
. Если 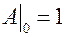 , то
, то 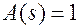 , что и доказывает лемму.
, что и доказывает лемму.
Вернемся к уравнениям Френе. Сведем их к одному уравнению третьего порядка
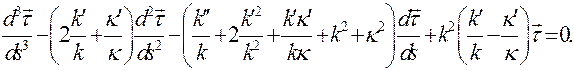
Общее решение этого уравнения содержит три произвольные вектора 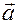 ,
, 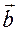 и
и 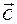 , как постоянные интегрирования. Следовательно,
, как постоянные интегрирования. Следовательно,
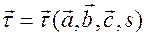 .
.
Воспользуемся этими векторами, чтобы удовлетворить следующим начальным условиям: 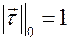 (этого всегда возможно добиться вследствие однородности уравнения),
(этого всегда возможно добиться вследствие однородности уравнения), 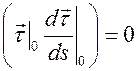 ,
, 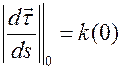 ,
, 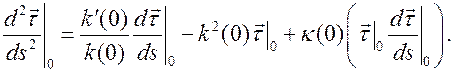 Подставляя решение
Подставляя решение 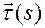 в уравнения Френе, находим
в уравнения Френе, находим
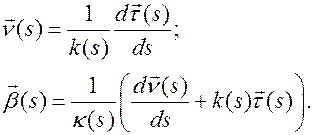
Полученное решение уравнений Френе удовлетворяет условиям ортонормированности репера Френе в каждой точке кривой, а произвол, определяемый векторами 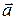 ,
, 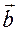 и
и 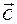 сузился только до произвола в выборе направлений векторов
сузился только до произвола в выборе направлений векторов 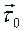 и
и 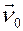 в начальной точке при условии
в начальной точке при условии 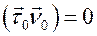 . После интегрирования уравнения
. После интегрирования уравнения
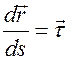
получаем
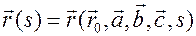 ,
,
где 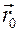 постоянный вектор интегрирования последнего уравнения. Таким образом, вектор
постоянный вектор интегрирования последнего уравнения. Таким образом, вектор 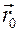 и вектора
и вектора 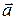 ,
, 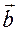 и
и 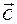 при указанных выше условиях определяют положение начальной
при указанных выше условиях определяют положение начальной  точки кривой в пространстве и положение кривой.
точки кривой в пространстве и положение кривой.
Найдем угловую скорость вращения репера Френе. С одной стороны, согласно выражению (3.13) мы имеем
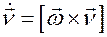 ,
,
где 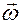 - угловая скорость вращения репера Френе. С другой стороны из второго уравнения Френе находим
- угловая скорость вращения репера Френе. С другой стороны из второго уравнения Френе находим
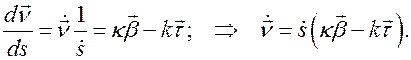
Сравнивая последние два выражения, получаем следующее равенство
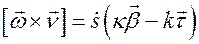 .
.
Помножим полученное равенство векторно на 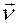 .Тогда будем иметь
.Тогда будем иметь
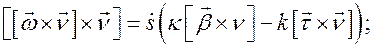
Откуда, раскрывая векторные произведения, получаем
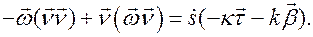
Повторяя эти же рассуждения для вектора 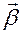 , находим
, находим
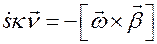 .
.
Откуда следует, что 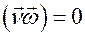 . Подставляя этот результат в соотношение (6.9), находим угловую скорость вращения репера Френе
. Подставляя этот результат в соотношение (6.9), находим угловую скорость вращения репера Френе
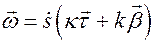
Вернемся к уравнениям Френе. Найдем траекторию частицы, если кривизна и кручение постоянны, т.е. 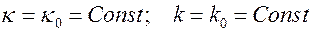 .
.
Интегрируем уравнения Френе для этого случая. Дифференцируя второе уравнение Френе, и, пользуясь остальными уравнениями, получаем
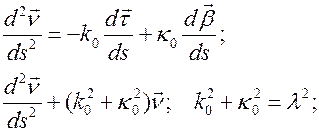
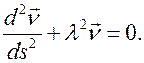
Мы получили векторное волновое уравнение, решение которого имеет вид
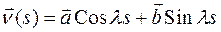
где 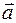 и
и 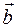 - векторные константы интегрирования. Подставляя полученное решение в первое и третье уравнения Френе, находим недостающие решения
- векторные константы интегрирования. Подставляя полученное решение в первое и третье уравнения Френе, находим недостающие решения
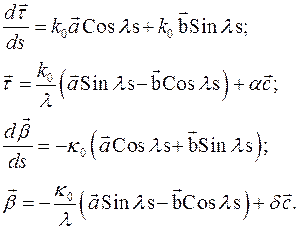
Видно, что постоянные интегрирования 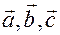 носят векторный характер и определяются из условий, налагаемых на вектора репера Френе
носят векторный характер и определяются из условий, налагаемых на вектора репера Френе
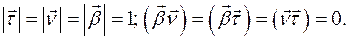
Из этих условий получаем
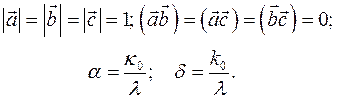
Следовательно, решения уравнений Френе имеют вид
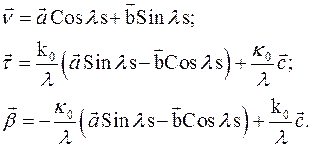
Уравнение кривой, в силу определения 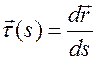 , имеет вид
, имеет вид
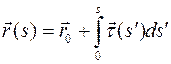 ,
,
где 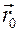 - граничное значение радиус – вектора. Подставляя в это выражение найденное решение (4.11), получаем уравнение траектории частицы
- граничное значение радиус – вектора. Подставляя в это выражение найденное решение (4.11), получаем уравнение траектории частицы
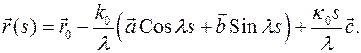
Поскольку репер 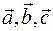 неподвижен и ортонормирован - его можно отождествить с координатным декартовым репером и увидеть, что мы получили уравнение винтовой линии – линии постоянной кривизны и кручения. Ось линии направлена по вектору
неподвижен и ортонормирован - его можно отождествить с координатным декартовым репером и увидеть, что мы получили уравнение винтовой линии – линии постоянной кривизны и кручения. Ось линии направлена по вектору 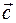 . Радиус винтовой линии
. Радиус винтовой линии 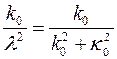 , а шаг винта
, а шаг винта 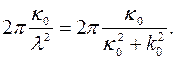
 2015-07-04
2015-07-04 2914
2914