2015-07-04
1529
В дальнейшем мы будем отождествлять с рассматриваемым пространством совокупность чисел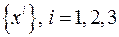 
, причем таким образом, что каждой точке пространства поставим в соответствие 3 числа, которые будем называть координатами пространственной точки. Такое соответствие должно быть взаимно однозначным. Выделим в нашем пространстве систему кривых, при движении вдоль каждой из которых будет меняться только одна координата, а остальные будут оставаться постоянными. Эти кривые мы будем называть координатными кривыми, а конгруэнцию (объединение) этих кривых будем называть системой координат.
Пример: конгруэнции трех прямых – декартова система;
Конгруэнции окружности и двух прямых – цилиндрическая система;
Конгруэнции двух окружностей и прямой – сферическая система.
Точка пространства определяется в этом случае как точка пересечения трех координатных кривых. Три касательные к координатным кривым вектора в точке пересечения составляют координатный репер. Таким образом, каждой системе координат ставится в соответствие бесконечное множество координатных (базисных) реперов. Это соответствие взаимно однозначное.
|
|
|
Произвольные векторы в координатных базисах описываются всеми соотношениями, полученными нами выше. В дальнейшем мы будем отличать координатные базисы от всех остальных переобозначением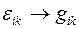 
, где 
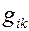- метрический тензор. Таким образом, если 
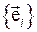- координатный базис, то
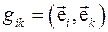
Координатные базисы играют в геометрии пространства особую роль. Действительно, рассмотрим две точки пространства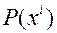 
и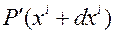 
. Вектор 
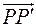, соединяющий эти точки, при 
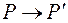имеет контравариантные компоненты 
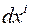. То есть, в координатном базисе этот вектор будет иметь вид 
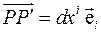. Запишем квадрат модуля этого вектора:
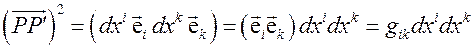(4.2)
Видно, что мы получили квадратичную форму
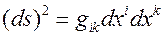, (4.3)
где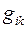 
- метрический тензор. Знание метрического тензора и квадратичной формы позволяет в координатной системе легко восстановить координатный базис:
1. Направление базисного вектора является касательным к координатной линии;
2. Квадрат его модуля и углы между базисными векторами находятся из определения метрического тензора;
Положим, что мы имеем две координатные системы, связанные друг с другом преобразованиями
. (4.4)
Тогда, используя формальный прием перехода от одних независимых переменных к другим, мы можем записать
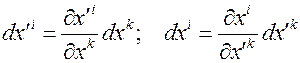(4.5)
В дальнейшем будем полагать, что преобразования координат (4.4) взаимно однозначны. В силу взаимной однозначности преобразований, мы будем иметь
,
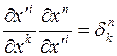откуда следует, что матрица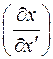 
является обратной к матрице 
.
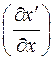Сопоставим полученные выше выражения (3.20)
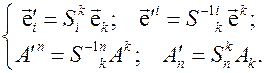
с преобразованиями (4.5). Нетрудно увидеть, что преобразования координат и координатных базисов эквивалентны преобразованиям базисов, рассмотренных в разделе 3, осуществляемых матрицей
|
|
|
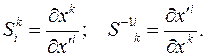(4.6)
Приведем основные положения изложенной выше теории:
1. Геометрия пространства в произвольной системе координат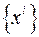 
определяется его квадратичной формой 
;
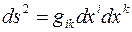2. Система координат 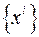и координатный базис 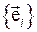в каждой точке пространства взаимно однозначно определяют друг друга:
а) направление вектора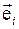 
является касательным к 
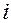- й координате;
б) модули векторов базиса и углы между ними определяются формулой
;
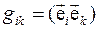в) координатные линии системы координат являются огибающими соответствующего вектора координатного базиса.
3. Координатный базис 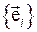и дополняющий его базис 
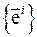взаимно
однозначно определяют друг друга:
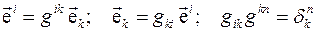
4.Любой вектор может быть представлен как своими ковариантными, так и контравариантными компонентами
.
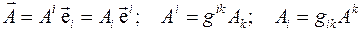Соответствующие компоненты вектора определяются в координатных
базисах стандартным способом
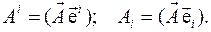
5. Для любых векторов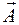 
и 
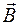в координатном базисе скалярное
произведение будет иметь вид
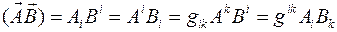
6. Если две системы координат 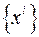и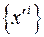 
связаны между собой
взаимно однозначным преобразованием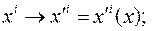 
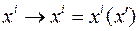тогда
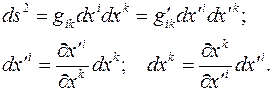
И матрица преобразования координат будет иметь вид
.
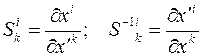7. Координатные базисы различных систем координат между собой
связаны соотношениями:
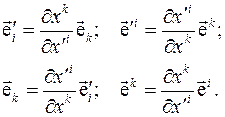
8. Компоненты вектора в координатных базисах различных систем
координат между собой связаны соотношениями
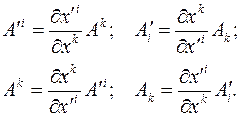
Рассмотрим следующие примеры.
1. Выразить скорость и ускорение материальной точки в декартовой системе координат.
