По определению скорость 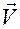 и ускорение
и ускорение 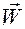 материальной точки находятся как
материальной точки находятся как
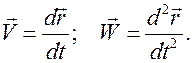
Положим, что 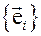 - координатный репер декартовой системы координат.
- координатный репер декартовой системы координат.
Тогда радиус – вектор 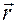 материальной частицы может быть представлен в виде разложения по этому координатному базису. А именно,
материальной частицы может быть представлен в виде разложения по этому координатному базису. А именно,
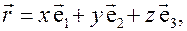
где 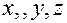 - контравариантные компоненты радиуса – вектора
- контравариантные компоненты радиуса – вектора 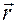 в координатном базисе декартовой системы координат. Поскольку координатный базис декартовой системы координат не зависит от точки пространства, применяя определения скорости и ускорения материальной точки, получим
в координатном базисе декартовой системы координат. Поскольку координатный базис декартовой системы координат не зависит от точки пространства, применяя определения скорости и ускорения материальной точки, получим
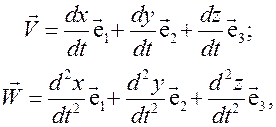
где 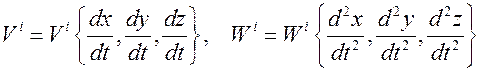 контравариантные компоненты векторов скорости и ускорения, соответственно. Если ввести обозначения
контравариантные компоненты векторов скорости и ускорения, соответственно. Если ввести обозначения 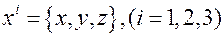 , тогда выражения для скорости и ускорения материальной точки можно записать в более компактном виде
, тогда выражения для скорости и ускорения материальной точки можно записать в более компактном виде
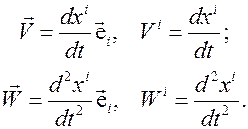
Поскольку в случае декартовой системы координат основной и дополняющий координатные базисы совпадают, т.е. 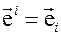 , нетрудно выписать и ковариантные компоненты векторов скорости и ускорения материальной точки
, нетрудно выписать и ковариантные компоненты векторов скорости и ускорения материальной точки
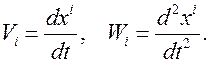
2.Выразить скорость 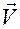 и ускорение
и ускорение 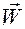 материальной точки в цилиндрических координатах.
материальной точки в цилиндрических координатах.
|
|
|
 2015-07-04
2015-07-04 398
398








