Численные методы решения нелинейных уравнений.
Описание методов
Метод хорд.
Если на отрезке изоляции корня 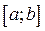 уравнения
уравнения 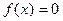 выполняются следующие условия:
выполняются следующие условия:
 1)
1) 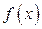 ,
, 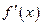 ,
, 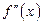 непрерывны;2)
непрерывны;2) 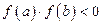 ;
;
3) 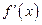 и
и 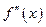 сохраняют знак,
сохраняют знак,
то можно определить последовательность точек, сходящуюся к исходному корню.
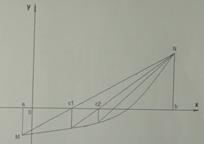
Метод хорд состоит в том, что в качестве начального приближения берётся одна из границ отрезка изоляции корня, а в качестве приближения 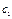 – точка пересечения оси ОХ с хордой графика, проведённой через точки
– точка пересечения оси ОХ с хордой графика, проведённой через точки 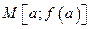 и
и 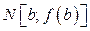 . Таким образом, дуга графика принимается за отрезок прямой, т.е. производится линейная интерполяция (рис.).
. Таким образом, дуга графика принимается за отрезок прямой, т.е. производится линейная интерполяция (рис.).
Для нахождения точки 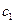 используется уравнение хорды MN:
используется уравнение хорды MN: 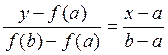 .
.
Откуда 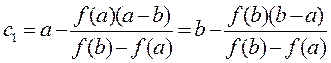 .
.
Следующие приближения находятся из формулы
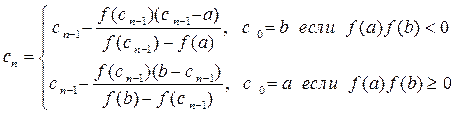 .
.
Если необходимо, это построение можно повторить.
Схема метода хорд:
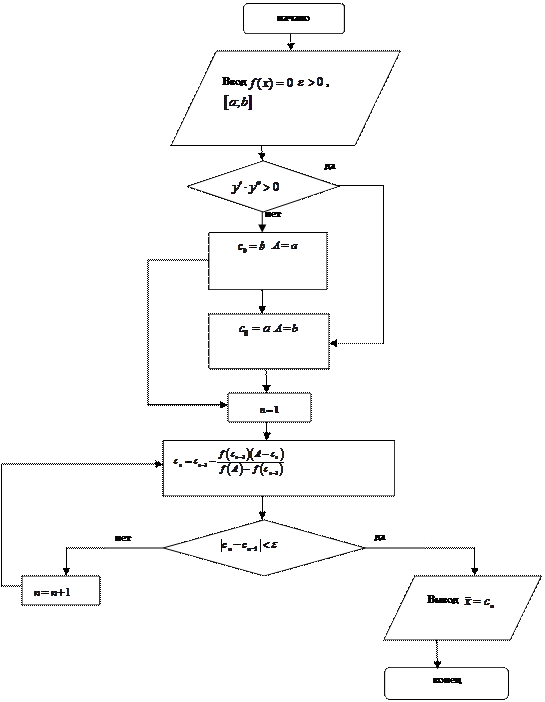 |
Метод касательных (метод Ньютона).
Пусть на отрезке изоляции корня 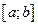 уравнения
уравнения 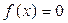 выполняются следующие условия:
выполняются следующие условия:
 1)
1) 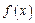 ,
, 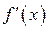 ,
, 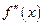 непрерывны;
непрерывны;
2) 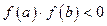 ;
;
3) 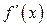 и
и 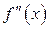 сохраняют знак.
сохраняют знак.
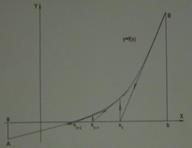
Идея метода состоит в том, что в одном из концов дуги АВ графика 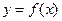 проводится касательная к этой дуге, и в качестве приближённого значения корня выбирается
проводится касательная к этой дуге, и в качестве приближённого значения корня выбирается 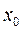 абсцисса точки пересечения этой касательной с осью ОХ (рис.). Как известно, уравнение касательной к кривой
абсцисса точки пересечения этой касательной с осью ОХ (рис.). Как известно, уравнение касательной к кривой 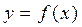 в точке
в точке 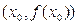 имеет вид
имеет вид 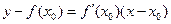 .
.
Следовательно,
уравнение касательной в точке 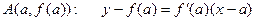 ,
,
уравнение касательной в точке 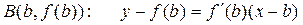 .
.
Абсцисса точки пересечения касательной с осью ОХ определяется по формуле
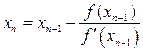 .
.
Итерационный процесс прекращают, если 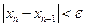 , тогда приближённое значение корня полагают равным
, тогда приближённое значение корня полагают равным 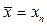 .
.
Перед началом процесса вычисления необходимо проверить правильность отделения корня. Для этого необходимо узнать знак произведения значений функции и её второй производной на каждом из концов выбранного отрезка. Если в обоих случаях знак будет отрицательной, то отрезок выбран неправильно, и решение уравнения найдено не будет.
Начальное приближение выбирается из следующих условий:
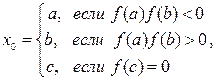 где
где 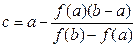 .
.
Условия сходимости метода Ньютона:
1. 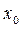 выбрано достаточно близко к корню уравнения
выбрано достаточно близко к корню уравнения 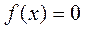 .
.
2. Производная 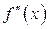 не становится очень большой.
не становится очень большой.
3. Производная 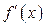 не слишком близка к нулю (никакие два корня не находятся слишком близко друг к другу).
не слишком близка к нулю (никакие два корня не находятся слишком близко друг к другу).
Схема метода касательных:
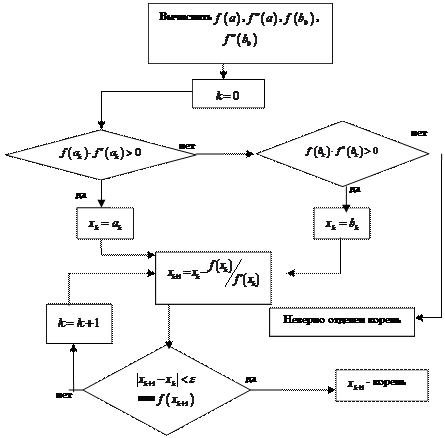 |
Задание: решить уравнение 
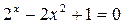 методом хорд и методом Ньютона.
методом хорд и методом Ньютона.
 2015-07-04
2015-07-04 4321
4321