Приближенные формулы

При больших n непосредственное вычисление вероятностей P_n(m) по формуле Бернулли сопряжено с трудностями вычислительного порядка, поэтому в таких случаях используют различные варианты приближенных вычислений, основанные на предельных теоремах Пуассона и Муавра‑Лапласа.

А. Приближенная формула Пуассона используется в том случае, когда число испытаний Бернулли (n) – велико, а вероятность успеха в отдельном испытании мала (p<0,1). Тогда

P_n(m)»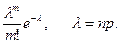

Задача 5. Известно, что процент брака для некоторой детали равен 0,5%. Контролер проверяет 1000 деталей. Какова вероятность обнаружить ровно 3 бракованных детали? Какова вероятность обнаружить не меньше 3-х бракованных деталей?

Решение. Имеем 1000 испытаний Бернулли с вероятностью «успеха» р=0,005, и npq <5. Применяя пуассоновское приближение с np=5, получаем

P₁₀₀₀(3)» 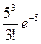, P₁₀₀₀(m³3)=1-P₁₀₀₀(m<3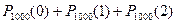)= 1-[ ]»1- 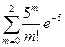и по таблицам находим Р₁₀₀₀(3)»0,14, Р₁₀₀₀(m³3)»0,875.

В силу определенной «симметричности» понятий «успех» и «неудача» приближенная формула Пуассона может использоваться в схеме независимых испытаний Бернулли также и в случае, когда р близко к единице (т.е. q<0,1), а nq - не велико и не мало:

P_n(n-m)=C_n^n-mp^n-mq^m=C_n^mp^n-mq^m »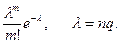

Б. Приближенные формулы Муавра – Лапласа. Если в схеме независимых испытаний Бернулли число испытаний n велико, а вероятности успеха и неудачи не малы (например, 0,1<p<0,9), то вероятность P_n(m) появления ровно m успехов в n испытаниях вычисляется по формуле (локальная теорема Муавра-Лапласа):

P_n(m)=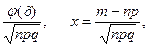

где j(х)= 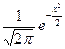. Функция j(х) – четная и для положительных значений х составлена таблица ее значений.

Задача 6. Вероятность поражения мишени стрелком при одном выстреле р=0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

Решение. Здесь n=10, m=8, p=0,75, q=0,25. Найдем х= 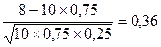, и по таблице определяем j (x)=0,3739, тогда искомая вероятность равна

Р₁₀(8)= .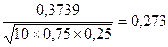

Для вычисления вероятности P_n(m₁,m₂)= P(m₁£m£m₂) события, состоящего в том, что число успехов в n испытаниях Бернулли окажется заключенным в пределах от m₁ до m₂, используется следующая приближенная формула (интегральная теорема Муавра-Лапласа):

P_n(m₁,m₂)»Ф(x₂)‑Ф(x₁),

где x₁= 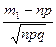, x₂= 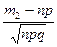, а Ф(х)= 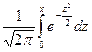- функция Лапласа.

Функция Ф(x) равна 0 при x=0; Ф(-х)º-Ф(x) для всех x, то есть симметрична относительно x=0. Для функции Ф(х) составлены специальные таблицы при положительных значениях аргумента.

Задача 7. Вероятность появления события А в каждом из 21 независимых испытания равна 0,7. Найти вероятность того, что событие А появится в большинстве испытаний.

Решение. х₁= 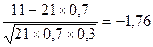. Аналогично подсчитывается х₂ = 3. Тогда Р(11£m£21)=Ф(х₂)–Ф(х₁)=0,49865+0,4608=0,9594.

Используя интегральную формулу Муавра-Лапласа можно вычислить вероятность того, что частота появления успеха в n независимых испытаниях Бернулли (т.е. число m/n) отклонится от вероятности успеха не более чем на положительную величину e: .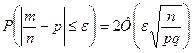

Задача 8. Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число e, чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его вероятности не превышала e.

Решение. В этом примере p=0,8, n=400. По условию задачи 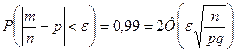. Следовательно, 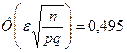, По таблице для функции Лапласа определяем 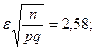и значит, e=0,0516.

Приближенную формулу можно использовать и в следующей «урновой» схеме: из генеральной совокупности объема N, содержащей М белых и N-M черных шаров, осуществляется последовательный выбор без возвращения n элементов. Вероятность того, что в полученной выборке окажется ровно m белых шаров, вычисляется по формуле

P_M,N(m,n)= .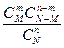

Если объем генеральной совокупности и число белых шаров достаточно велики (N®¥, M®¥, M/N®p=const), то «урновую» схему можно приближенно заменить схемой Бернулли:

P_M,N(m,n)»P_n(m), где P_n(m)=C_n^mp^mq^n-m