Приближенные числа и действия над ними. Оценка точности вычисления

Величиной называется то, что может быть в определенных единицах выражено числом. Например, длина, площадь, объем – это величины. Значение величины, в истинности которого мы не сомневаемся, называется точным (в дальнейшем х - точное число). Но обычно на практике, отыскивая значение какой-либо величины, получают лишь ее приближенное значение (в дальнейшем а - приближенное число). Например, при измерении физических величин с помощью измерительных приборов.

Модуль разности точного и приближенного значений величины называется абсолютной погрешностью приближения 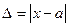Предельной абсолютной погрешностью приближения или границей погрешности или оценкой абсолютной погрешности называется число 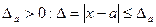. Таких оценок может быть бесконечное число. Лучшей оценкой погрешности является наименьшая оценка.

Краткая запись точного числа: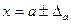

Отношение абсолютной погрешности приближения к модулю точного значения величины называется относительной погрешностью 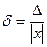. На практике используется 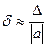Для предельной относительной погрешности (оценки относительной погрешности): 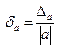. Относительная погрешность обычно выражается в %.

В дальнейшем слово оценка опускается.

ПРИМЕР. Найти абсолютную и относительную погрешность приближения а=3,14 для х=π.

Известно, что 3,14 < π<3,15.

Отсюда следует, что 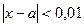, т.е.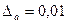

Если учесть, что 3,14 < π<3,142, то получим лучшую оценку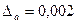

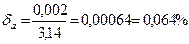
Цифра в десятичной записи приближенного значения величины х называется верной в широком смысле, если абсолютная погрешность приближения не превосходит единицы того разряда r, которому принадлежит эта цифра 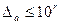(Нулевым разрядом считается разряд единиц, десятичные цифры считаются отрицательными разрядами). Существует еще понятие верной цифры в узком смысле: 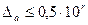. В дальнейшем будем рассматривать верные цифры в широком смысле. Остальные цифры числа называются сомнительными. Значащими цифрами числа, записанного в десятичной форме, называются все верные цифры числа, начиная с первой слева, отличной от 0. Все нули слева являются незначащими. По количеству значащих цифр можно легко оценить абсолютную погрешность приближенного числа. За оценку абсолютной погрешности можно взять 0,5 разряда, следующего за последней значащей цифрой. Предельную относительную погрешность можно принять равной дроби, числитель которой 1, а знаменатель – удвоенное целое число, записанное при помощи всех значащих цифр данного числа.

ПРИМЕР. а=0,065;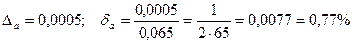

ЗАДАЧА 1.1. Объем помещения V определен с предельной относительной погрешностью δ Сколько значащих цифр в V?

V=503м3	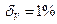РЕШЕНИЕ.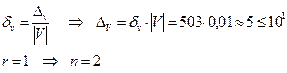
n –?

V=500±5

ЗАДАЧА 1.2. Известно, что приближенное значение а имеет n значащих цифр. Оценить абсолютную и относительную погрешность.

a=0,0359 n=2	РЕШЕНИЕ.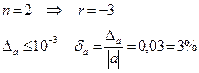

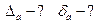ЗАДАЧА 1.3. Округлите сомнительные цифры приближенного числа а, если известна относительная погрешность δ

а=0,6594	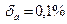РЕШЕНИЕ.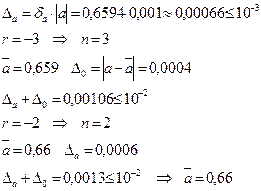

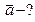Задание 1.1.

Известно, что приближенное значение а имеет n значащих цифр. Оценить абсолютную и относительную погрешность со следующими исходными данными.

	a=295,3 n=2, n=3, n=4

Задание 1.2.

Округлите сомнительные цифры приближенного числа а, если известна относительная погрешность δ

а=694,6 ,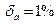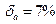

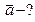В теории приближенных вычислений рассматриваются два вида задач: прямая и обратная.

Прямая задача. Выполнить действия над приближенными числами при заданных погрешностях приближений. Оценить погрешность полученного результата.

Обратная задача. Выполнить действия над приближенными числами при заданной погрешности результата. Установить, какими должны быть погрешности исходных приближений.

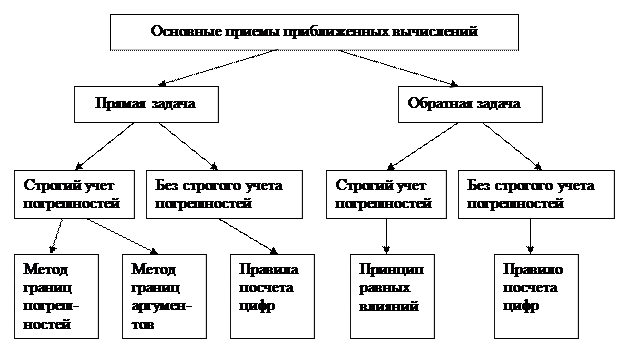
Правила подсчета цифр для прямой задачи

1. В алгебраической сумме приближенных значений, в записи которых все цифры верны, следует оставлять столько десятичных знаков, сколько их имеет слагаемое с наименьшим числом десятичных знаков. Слагаемые с большим числом десятичных знаков следует предварительно округлить, оставив на один десятичный знак больше, чем у выделенного слагаемого.

2,3+4,681=2,3+4,68=6,98≈7,0

2. В произведении приближенных значений следует оставлять столько значащих цифр, сколько их имеет сомножитель с наименьшим количеством значащих цифр. Сомножители с большим числом значащих цифр следует предварительно округлить, оставив на одну значащую цифру больше, чем у выделенного сомножителя. Аналогично для деления.

23 ∙ 1,056 ≈ 23 ∙ 1,06 =24,38 ≈ 24; 10,1 ∙ 0,5 ≈ 5

3. При возведении приближенного числа в степень или при извлечении корня в результате следует оставлять столько значащих цифр, сколько их имеет основание степени или подкоренное число.

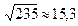
4. При выполнении последовательного ряда действий над приближенными числами в промежуточных результатах следует оставлять на одну цифру больше, чем рекомендуют предыдущие правила. В окончательном результате эта цифра отбрасывается по правилам округления.

Правило подсчета цифр для обратной задачи

Для того, чтобы в результате ряда промежуточных действий получить число с n верными цифрами, исходные данные следует брать с таким числом верных цифр, которые согласно предыдущим правилам обеспечивают n+1 верную цифру в результате. Окончательный результат округлить до n цифр.

Метод границ аргументов (МГА)

ДАНО: 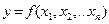- монотонная функция;

Приближенные значения аргументов и оценки погрешностей.

МЕТОД:

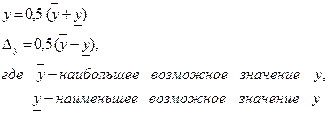
В результате оставляют верные цифры плюс 1 сомнительную (в соответствии с полученной погрешностью).

Метод границ погрешностей.

Оценка погрешности результата вычисляется как функция погрешностей исходных данных. Вывод формулы осуществляется по соотношениям, приведенным в таблице.

Таблица 1.1.

Действия над приближ.числами	Функция	Оценка абсолютной погрешности	Оценка относительной погрешности
Сложение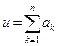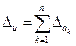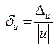
Умножение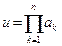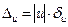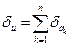
Деление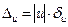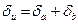
Степень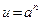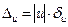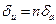
Корень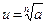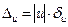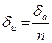

Принцип равных влияний.

Принцип заключается в том, что оценки погрешностей аргументов одинаково влияют на погрешность результата, т.е. считаются равными.

Замечания.

1. Правило четной цифры: если при округлении первая из отброшенных цифр =5, и за ней не следуют отличные от нуля цифры, то последняя цифра усиливается, если она нечетная, и остается без изменения, если она четная.

2. Приближенное значение а величины х называется недостаточным, если x>a и избыточным, если x<a.

3. Нули справа будут значащими, если они являются верными цифрами.

4. При вычислениях нижнюю границу можно округлять в сторону уменьшения, а верхнюю – в сторону увеличения.

5. Дополнительная цифра к промежуточному результату может быть добавлена только в том случае, если в арифметическом действии участвуют исходные данные.

ЗАДАЧА 1.4.

Стороны прямоугольника 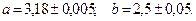Вычислить диагональ прямоугольника по формуле: 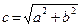и оценить погрешности вычислений.

1) Правило подсчёта цифр:

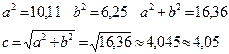
2) МГА:

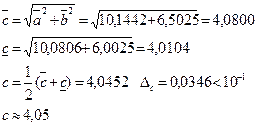
3) Метод границ погрешностей

Предварительно получив формулу, пользуясь таблицей 1.1., вычислим ∆_с

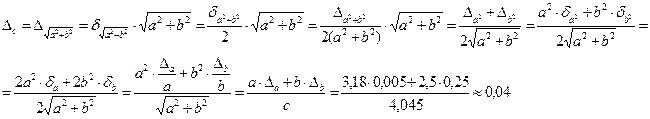Оценим ∆_с =0,04≤10^-1

Следовательно, верным в результате будет только 1 десятичный знак. Произведём вычисления по формуле и округлим результат, оставив 1 сомнительную цифру.

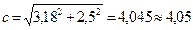
с=4,05±0,04

ЗАДАЧА 1.5. С каким числом верных знаков следует выбрать числа a и b, чтобы получить с в задаче 1.4. с одним верным знаком?

РЕШЕНИЕ.

По условию

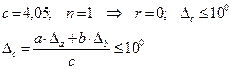
1) Принцип равных влияний

Примем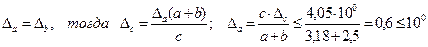

Следовательно, чтобы в задаче 1.4. получить результат с 1 верной цифрой, исходные данные можно брать без десятичных знаков.

2) Правило подсчета цифр

Искомый результат должен содержать одну значащую цифру, следовательно, при выполнении арифметических действий должно быть получено число с двумя значащими цифрами. Последним действием является извлечение корня, значит, значение подкоренного выражения также должно иметь две значащие цифры. В нашем случае это двузначное число, т.е. результат сложения не должен иметь десятичных знаков, а соответственно и слагаемые. Но слагаемыми являются квадраты исходных данных. Поэтому исходные данные следует брать без десятичных знаков.