Задача вычисления расстояния между двумя точками является метрической задачей. Метрические задачи, как правило, решают в
прямоугольной системе координат.
Задача. В прямоугольной системе координат даны точки А и В своими координатами. Вычислить расстояние между этими точками.
 Дано:
Дано:
R= (O,  )
)
А(xA;yA;zA)
B(xB;yB;zB)
Вычислить: │АВ│ Рис.5
Решение.
Заметим, что │ АВ │=│  │. Так как модуль вектора равен корню квадратному из суммы квадратов координат вектора, учитывая, что
│. Так как модуль вектора равен корню квадратному из суммы квадратов координат вектора, учитывая, что  = ={xB−xA; yB− yA; zB− zA}, получаем:
= ={xB−xA; yB− yA; zB− zA}, получаем:
 |
(3)
5. Деление отрезка в данном отношении.
Пусть дана прямая ℓ и точки А, В и С принадлежащие прямой ℓ.
Определение. Отношением, в котором точка С делит отрезок АВ называется число  . Обозначение λС=(АВ,С).
. Обозначение λС=(АВ,С).
Заметим, что в векторной алгебре не определяется операция деления вектора на вектор. Приведённая выше запись имеет смысл только для коллинеарных векторов. В данном случае это выполняется, так как точки А В и С лежат на одной прямой.

Число λ может принимать как положительные так и отрицательные значения. Так, на рис. 4 а) векторы 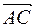 и
и 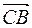 сонаправлены и, поэтому,
сонаправлены и, поэтому,
λ > 0; то есть точка С лежит на отрезке АВ. В случае, приведённом на рис.4б), 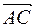 и
и 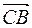 противоположно направлены и, следовательно, λ < 0, а точка С лежит вне отрезка АВ. Число λ не может принимать значение равное − 1, так как в этом случае
противоположно направлены и, следовательно, λ < 0, а точка С лежит вне отрезка АВ. Число λ не может принимать значение равное − 1, так как в этом случае 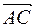 = −
= − 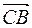 =>
=> 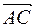 =
= 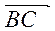 => А = В, что означает отрезов вырождается в точку.
=> А = В, что означает отрезов вырождается в точку.
 Задача. В аффинной системе координат даны точки А и В своими координатами и известно отношение, в котором точка С делит отрезок АВ. Вычислить координаты точки С.
Задача. В аффинной системе координат даны точки А и В своими координатами и известно отношение, в котором точка С делит отрезок АВ. Вычислить координаты точки С.
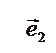 Дано: R=(О,
Дано: R=(О, 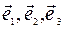 ).
).
А(xA;yA;zA), B(xB;yB;zB)
(АВ,С) = λС
Найти координаты т. С.
Решение
По определению  =>
=> 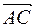 = λС*
= λС* 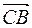 . Так как
. Так как 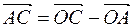
и  то
то  =>
=>  .
.
Векторы 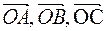 − радиус-векторы точек А, В, и С поэтому
− радиус-векторы точек А, В, и С поэтому
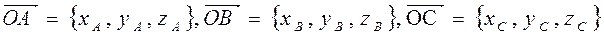 .
.
По теореме о координатах линейной комбинации векторов имеем:
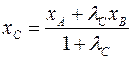 , , 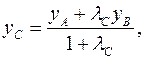 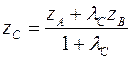 |
(4)
Следствие. Если точка С является серединой отрезка АВ, то λС = 1. => Середина отрезка имеет координаты
 , ,  , ,  . . |
(5)
 2015-07-04
2015-07-04 2184
2184








