Плоскость в пространстве

1. Различные уравнения плоскости.

а). Уравнение плоскости, заданной точкой М_о и вектором нормали.

При аксиоматическом построении геометрии плоскость считается

основным неопределяемым понятием, основные свойства которой определяются аксиомами и их свойствами.

В аналитической геометрии основным методом изучения свойств геометрических фигур является метод координат, основной особенностью которого является возможность каждой геометрической фигуре поставить в соответствие уравнение или неравенство и изучать свойство исследуемой фигуры на основе следствий, вытекающих из анализа полученного уравнения.

Определение. Вектор, перпендикулярный плоскости, называется вектором нормали плоскости. (Рис.9)

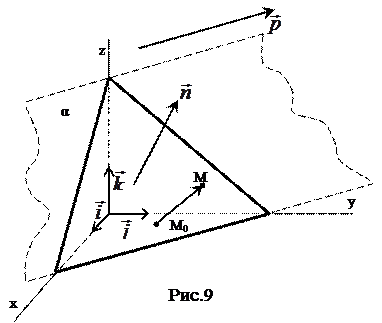
Поставим перед собой задачу получить уравнение плоскости в пространстве, заданной точкой и вектором нормали.

Введём пространстве прямоугольную систему координат и рассмотрим плоскость, заданную точкой М_о(х_о,у_о) и вектором 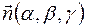перпендикулярным плоскости α. Приведённые данные определяют положение плоскости α в пространстве единственным образом.

Пусть точка М(x;y;z) − произвольная точка плоскости α. Очевидно, что точка М(x,y,z) 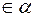тогда и только тогда, когда векторы 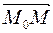и 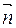взаимно перпендикулярны. => 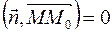. Координаты вектора 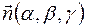и вектора 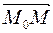(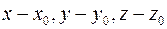) известны, =>

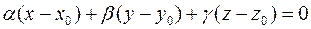
(6)

Уравнение (6) называется уравнением плоскости, заданной точкой М_о(х_о,у_о) и вектором нормали .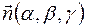

б). Условие параллельности вектора плоскости.

Теорема I. Вектор 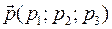параллелен плоскости α < =>

.

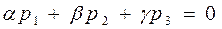Доказательство.

1. Необходимость.

Пусть вектор 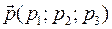параллелен плоскости α. (Рис.7) Тогда

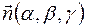и 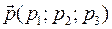перпендикулярны =>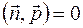

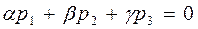
=> (7)

2. Достаточность.

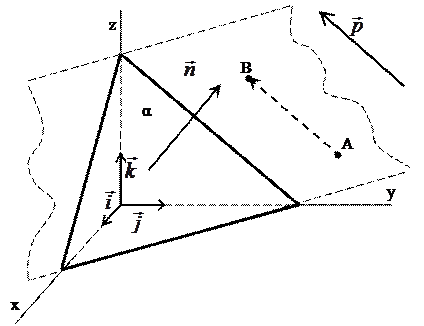
Пусть дан вектор даны вектор 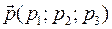и плоскость α своим уравнением 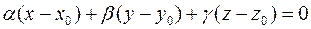. Кроме того пусть для координат вектора даны вектор 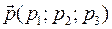выполнено условие 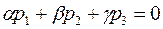. Возьмем в плоскости α некоторую точку А(х_А;у_А;z_А) принадлежащую плоскости α. Тогда координаты точки А удовлетворяют уравнению плоскости α, то есть

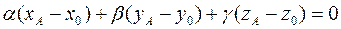. (8)

Отложим от точки А вектор, равный вектору 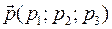и пусть его концом будет точка В(x_B;y_B;z_B). Очевидно, что для координат вектора 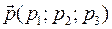справедливы соотношения: р₁= x_B−x_A; : р₂= y_B−y_A; : р₃= z_B−z_A. Подставив эти выражения для координат вектора даны вектор 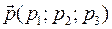в (9), получаем 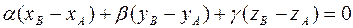. (9)

Сложив уравнение (8) с уравнением (9), получим

=>

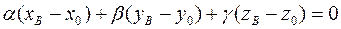Точка В принадлежит плоскости α, то есть вектор 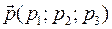║ α. Ч.т.д.