2015-07-04
3438
|
Пусть дана точка М0(x0,y0,z0) и два параллельных ей вектора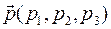 
и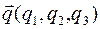 
составим уравнение этой плоскости δ.
Для определения координат вектора нормали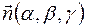 
этой плоскости поступим следующим образом.
а) Запишем уравнение плоскости δ, проходящей через точку М1 перпендикулярно некоторому вектору :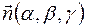
δ: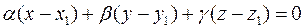 
.
б) Так как векторы 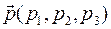и 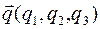параллельны плоскости δ, то воспользуемся условиям (7) параллельности этих векторов плоскости δ.
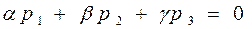
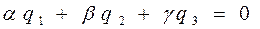
в) В результате получаем, что координаты вектора нормали плоскости δ должны являться решением системы уравнений:
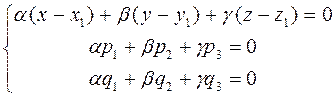(10)
Система уравнений (10)является системой линейных одноородных уравнений относительно неизвестных координат вектора нормали плоскости δ. Она имеет ненулевое решение, если определитель системы равен нулю. Таким образом, для плоскости, проходящей через точку М0 параллелно векторам 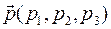и 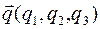должно выполняться условие
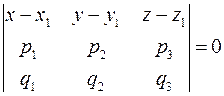. (11)
Соотношение (11) является уравнением относительно неизвестных x, y и z, которые являются координатами любой точки М(x;у;z) плоскости σ, его называют уравнением плоскости, проходящей через точку параллельно двум векторам.
|
|
|
в). Уравнение плоскости заданной тремя точками.
Согласно аксиомам геометрии через любые три точки пространства проходит единственная плоскость. Получим уравнение плоскости проходящей через три точки М1(x1;y1;z1), М2(x2;y2;z2), М3(x3;y3;z3).
|
Для решения этой задачи воспользуемся уравнением (11), считая, что
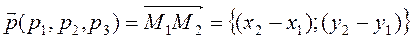, и
.
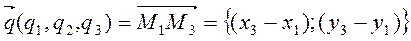В этом случае уравнение плоскости σ, проходящей через точки М1(x1;y1;z1), М2(x2;y2;z2), М3(x3;y3;z3), запишется в виде:
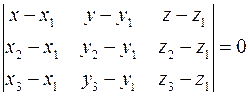(12)
Соотношение (12) это уравнение относительно неизвестных x, y и z, которые являются координатами любой точки М(x;у;z) плоскости σ, его называют уравнением плоскости, проходящей через три точки.
