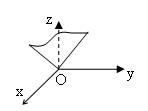
Напомним, что если аффинной системе координат задана плоскость α уравнением Ax+By+Cz+D=0 и вектор 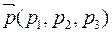 , то для того, чтобы вектор
, то для того, чтобы вектор 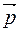 был параллелен плоскости α, необходимо и достаточно, чтобы выполнялось условие (7)
был параллелен плоскости α, необходимо и достаточно, чтобы выполнялось условие (7) 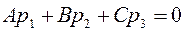 .
.
Рассмотрим частные случаи расположения плоскости α.
1) Пусть D=0. В этом случае координаты начала системы координат О(0;0;0) удовлетворяют уравнению плоскости α Ах+Ву+Сz=0. => плоскость проходит через начало координат.
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж | ||
| D=0 | Аx+By+Cz=0 |     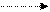   О(0;0;0) О(0;0;0) 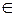 α α
| 
|
2) Пусть А=0, В≠0, С≠0 D≠0. Уравнение плоскости α будет иметь вид By+Cz+D=0. По теореме о параллельности вектора и плоскости, вектор
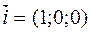 ‖ (Ох) => α ‖ (Ох).
‖ (Ох) => α ‖ (Ох).
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж | ||
| A=0 | By+Cz+D=0
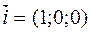 ‖ α ‖ α
| α ‖ (Ох) |
  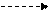     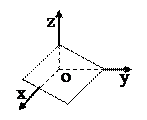
|
3) Пусть А≠0, В=0, С≠0, D≠0. Уравнение плоскости имеет Ах+Сz+ D =0.
В этом случае 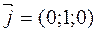 || α, поэтому α || Оу.
|| α, поэтому α || Оу.
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| B=0 | Аx+Cz+D=0
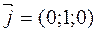 ‖ α ‖ α
| α ‖ (Оy) | 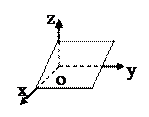
|
4) А≠0, В≠0, С=0, D≠0. Уравнение плоскости имеет вид Ах+Ву+D=0. В этом случае 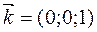 || α, поэтому α || Оz.
|| α, поэтому α || Оz.
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| C=0 | Аx+By+D=0
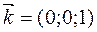 ‖ α ‖ α
| α ‖ (Оz) | 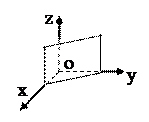
|
5) Пусть А=0, В≠0, С≠0 D=0. Уравнение плоскости имеет вид By+Cz=0 В этом случае координаты начала системы координат О(0;0;0) удовлетворяют уравнению плоскости α Ву+Сz=0 и вектор 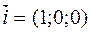 параллелен плоскости α. => Плоскость проходит через начало координат и параллельна оси Ох. => Плоскость проходит через ось Ох.
параллелен плоскости α. => Плоскость проходит через начало координат и параллельна оси Ох. => Плоскость проходит через ось Ох.
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| A=0,D=0 | Аx+By=0
О(0;0;0) 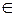 α α
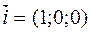 ‖ α ‖ α
| (Ох) 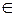 α α
|  
|
6) Пусть А≠0, В=0, С≠0, D=0. Уравнение плоскости имеет Ах+Сz =0. В этом случае координаты начала системы координат О(0;0;0) удовлетворяют уравнению плоскости α Ах+Сz=0 и вектор 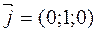 параллелен плоскости α. => Плоскость проходит через начало координат и параллельна оси Оу. => Плоскость проходит через ось Оу.
параллелен плоскости α. => Плоскость проходит через начало координат и параллельна оси Оу. => Плоскость проходит через ось Оу.
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| B=0,D=0 | Ax+Cz=0
О(0;0;0) 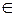 α α
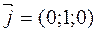 ‖ α ‖ α
| (Оy) 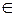 α α
| 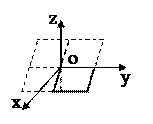
|
7) Пусть А≠0, В≠0, С=0, D=0. Уравнение плоскости имеет вид Ах+Ву=0. В этом случае координаты начала системы координат О(0;0;0) удовлетворяют уравнению плоскости α Ах+Ву=0 и вектор 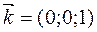 параллелен плоскости α. => Плоскость проходит через начало координат и параллельна оси Оz. => Плоскость проходит через ось Оz.
параллелен плоскости α. => Плоскость проходит через начало координат и параллельна оси Оz. => Плоскость проходит через ось Оz.
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| C=0,D=0 | Аx+By=0
О(0;0;0) 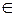 α α
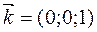 ‖ α ‖ α
| (Оz) 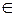 α α
| 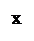 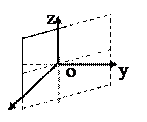
|
8) Пусть А=0, В=0, С≠0 D≠0. Уравнение имеет Сz+D=0,тогда векторы 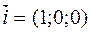 и
и 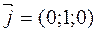 параллельны плоскости α => плоскость α |параллельна плоскости Оху. Если D≠0, то уравнение можно привести к виду z =N, где N≠0.
параллельны плоскости α => плоскость α |параллельна плоскости Оху. Если D≠0, то уравнение можно привести к виду z =N, где N≠0.
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| A=0,B=0 | Cz+D=0
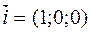 ‖ α ‖ α
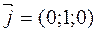 ‖ α ‖ α
| α ‖ (xОy) | 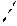    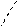              
|
9) Пусть А=0, В≠0, С=0 D≠0. Уравнение имеет 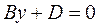 ,тогда векторы
,тогда векторы 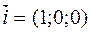 и
и 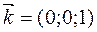 параллельны плоскости α. => α || (уОz). Если D≠0, то уравнение можно привести к виду у = N, N≠0.
параллельны плоскости α. => α || (уОz). Если D≠0, то уравнение можно привести к виду у = N, N≠0.
| Условие | Уравнение плоскости α | Расположение плоскости α |  Чертёж Чертёж
|
| A=0,С=0 | Ву+D=0
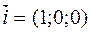 ‖ α ‖ α
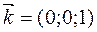 ‖ α ‖ α
| α ‖ (xОz) | 
|
10) Пусть А≠0, В=0, С=0 D ≠ 0. Уравнение имеет Ax +D = 0, тогда векторы 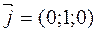 и
и 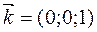 параллельны плоскости α => плоскость α || (Охz). Если D≠0, то уравнение можно привести к виду x = N, N≠0.
параллельны плоскости α => плоскость α || (Охz). Если D≠0, то уравнение можно привести к виду x = N, N≠0.
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| A=0,B=0 | Cz+D=0
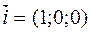 ‖ α ‖ α
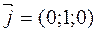 ‖ α ‖ α
| α ‖ (xОy) | 
|
11) Пусть А≠0, В=0, С=0 D=0. Уравнение имеет Ах=0. В этом случае координаты начала системы координат О(0;0;0) удовлетворяют уравнению плоскости α Ах=0 => О ϵ ɑ, так как В=0 и С=0 => α = Оуz.
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| B=0,C=0, D=0 | Аx=0 => x=0
О(0;0;0) 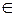 α α
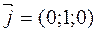 ‖ α ‖ α
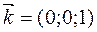 ‖ α ‖ α
| α = (yОz) | 
|
12) Пусть А=0, В=0, С≠0 D = 0. Уравнение имеет Сz=0, тогда векторы 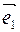 и
и 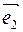 параллельны плоскости α и координаты начала системы координат О(0;0;0) удовлетворяют уравнению плоскости α => плоскость α = (Оху).
параллельны плоскости α и координаты начала системы координат О(0;0;0) удовлетворяют уравнению плоскости α => плоскость α = (Оху).
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| A=0,B=0,D=0 | Cz=0 => z=0
О(0;0;0) 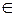 α α
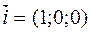 ‖ α ‖ α
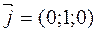 ‖ α ‖ α
| α = (xОy) | 
|
13) Пусть А≠0, В=0, С=0 D = 0. Уравнение имеет Ax=0, тогда векторы 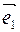 и
и 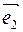 параллельны плоскости α и координаты начала системы координат О(0;0;0) удовлетворяют уравнению плоскости α => плоскость α = (Охz).
параллельны плоскости α и координаты начала системы координат О(0;0;0) удовлетворяют уравнению плоскости α => плоскость α = (Охz).
| Условие | Уравнение плоскости α | Расположение плоскости α | Чертёж |
| A=0,C=0, D=0 | By=0 => y=0
О(0;0;0) 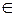 α α
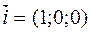 ‖ α ‖ α
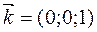 ‖ α ‖ α
| α = (xОz) |  
|
 2015-07-04
2015-07-04 1595
1595
