Взаимное расположение двух плоскостей

Теорема IV. Пусть в некоторой аффинной системе координат даны плоскости α: А₁ х+В₁ у+С₁ z+D₁ =0 и β: А₂ х+В₂ у+С₂ z+D₂ =0. Тогда:

1) α = β <= > А₁, В₁, С₁, D₁ и А₂, В₂, С₂, D₂ - пропорциональны, то есть: ,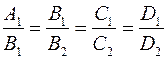

2) α ‖ β <= >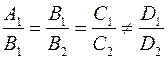

3) α ∩ β ≠ Ø <= > А₁, В₁, С₁, D₁ и А₂, В₂, С₂, D₂ - не пропорциональны.

Доказательство.

1) Необходимость.

Пусть для плоскостей α и β выполнено условие 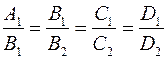=λ или А₁ = λ А₂ ; В₁ = λ В₂ ; С₁= λ С₂; D₁= λ D₂. Это означает, что уравнение плоскости α можно записать в виде: λ(А₂ х+В₂+ у+С₂z+D₂) =0<=> любая точка плоскости β принадлежит плоскости α то есть эти плоскости совпадают.

Достаточность.

Пусть α = β = > векторы нормали плоскостей α и β коллинеарны, то есть А₁ = λ А₂ ; В₁ = λ В₂ ; С₁= λ С₂. Это означает, что уравнение плоскости α можно записать в виде: λ(А₂ х+В₂ у+С₂z)+D₁ =0. = > D₁ = - λ(А₂ х+В₂ у+С₂z) = λD₂ = > А₁ = λ А₂ ; В₁ = λ В₂ ; С₁= λ С₂; D₁= λ D₂.

2) Необходимость.

Пусть для плоскостей α и β выполнено условие 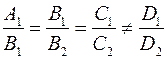. В этом случае векторы нормали плоскостей α и β коллинеарны, а значит плоскости α и β параллельны, но не совпадают, так как для совпадения плоскостей α и β необходимо и достаточно, что бы .

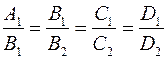Достаточность.

Пусть α ‖ β. = > что векторы нормал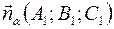и и 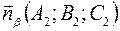коллинеарны, а это значит, что А₁ = λ А₂ ; В₁ = λ В₂ ; С₁= λС₂, но D₁≠ λD₂так α ≠ β.

3) Необходимость.

Пусть α ∩ β ≠ Ø. = > что векторы нормали 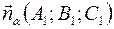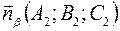не коллинеарны, а это значит, что А₁, В₁, С₁ и А₂, В₂, С₂ - не пропорциональны.

Достаточность.

Пусть А₁, В₁, С и А₂, В₂, С₂ - не пропорциональны. = > что векторы нормали 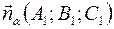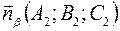неколлинеарны, а это значит, что > А₁, В₁, С₁, ₁ и А₂, В₂, С₂, - не пропорциональны.

Лекция №3

4.Геометрический смысл знака многочлена Ах+Ву+Сz+D.

Теорема III. Если в аффинной системе координат дана плоскость α: Ах+Ву+Сz+D=0, и точка М₁(x₁;y₁;z₁),координаты которой удовлетворяют неравенству Ах₁+ Ву₁+ Сz₁+D > 0, то точка М₁ лежит по одну сторону от плоскости α с концом вектора 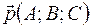, если его начало приложить к некоторой точке плоскости. Если координаты и точки М₁(x₁;y₁;z₁) удовлетворяют неравенству Ах₁+ Ву₁+ Сz₁+D< 0, то точка М₁ с концом вектора 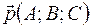лежит по разные стороны от плоскости α, если начало вектора приложить к некоторой точке плоскости.

Доказательство.

Прежде, чем привести доказательство сформулированной теоремы, заметим, что вектор 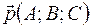не параллелен плоскости α. Для того чтобы убедиться в этом проверим условие параллельности вектора 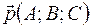плоскости α: А² + В² + С² ≠ 0.

Пусть в пространстве введена аффинная система координат R=(О 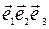) и дан многочлен Ах+ Ву+ Сz+D. Если в этот многочлен подставит координаты точки М₁, то значением этого многочлена буде некоторое число δ. Возможны следующие случаи: .

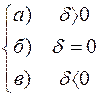В случае б) точка М₁ принадлежит плоскости α. Выясним, где находится точка М₁ в двух остальных случаях.

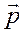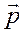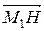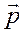Проведём через точку М₁ прямую М₁Н параллельно вектору , Тогда так как ‖ , то =λ· 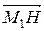=> х_Н - х₁ = λА; у_Н - у₁ = λВ; z_Н - z₁ = = λС. => х₁ = λА + х_Н ; у₁ = λВ + у_Н ; z₁ = λС + z_Н (13)

Подставив выражения для x₁; y₁ и z₁ в многочлен Ax + By + Cz + D, получаем: δ = Ax₁ + By₁ + Cz ₁+ D = λ(А² + В² +C²) + Ax_H + By_H + Cz_H + D.

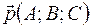Так как точка Н принадлежит плоскости α, то сумма подчёркнутых слагаемых равна 0. Таким образом δ = λ(А² + В² +C²). Отсюда получаем, что знак δ зависит от знака λ. => Если λ > 0, то вектор и вектор 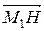сонаправлены и их концы расположены по одну сторону от плоскости α. Если λ < 0, то вектор 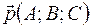и вектор 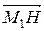противоположно направлены и их концы расположены по разные стороны от плоскости α. (Рис.11).

Рис.11

Теорема доказана.