Угол между двумя прямыми в пространстве

Об угле между прямыми в пространстве можно говорить в двух случаях: если прямые пересекаются и если они скрещиваются.

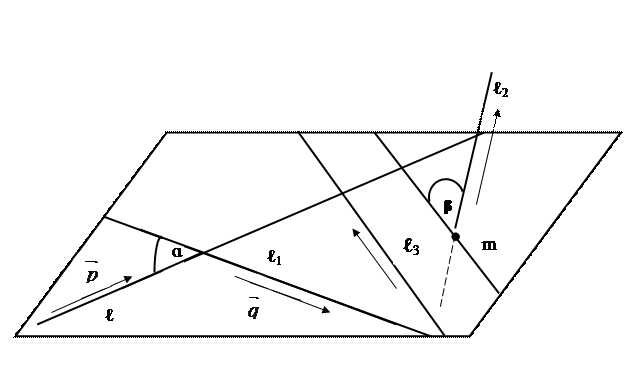
Пересекающиеся прямые l и l₁ образуют две пары вертикальных углов. В этом случае углом между прямыми называют один из пары меньших вертикальных углов.

Если прямые скрещиваются (l₂ и l₃), то в углом между прямыми называется угол между пересекающимися прямыми (l₂ и m), который получается в результате параллельного переноса одной из прямых (l₃) так, чтобы она пересекала вторую прямую.

В обоих случаях, угол между прямыми равен углу между направляющими векторами этих прямых 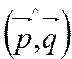или 180⁰ - .

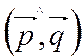Пусть направляющие вектора прямых заданы своими координатам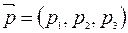и и .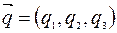

Тогда для вычисления величины угла между прямыми получаем формулу:

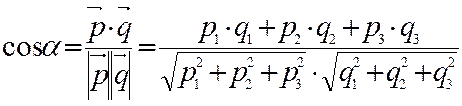(21)