Взаимное расположение прямой и плоскости

Пусть d – прямая. Точка 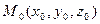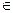d и направляющий вектор 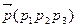. Плоскость α задана уравнением: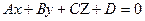

Возможны следующие случаи взаимного расположения прямой и плоскости:

1) Прямая пересекает плоскость, то есть: d ∩α = N. В этом случае прямая и плоскость имеют одну общую точку.

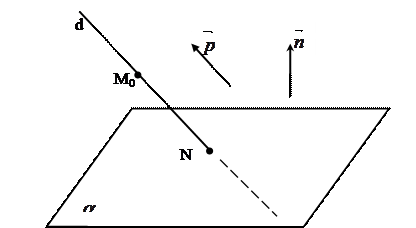
Рис. 17

2) Прямая параллельна плоскости, то есть: d || α. В этом случае прямая и плоскость не имеют общих точек.

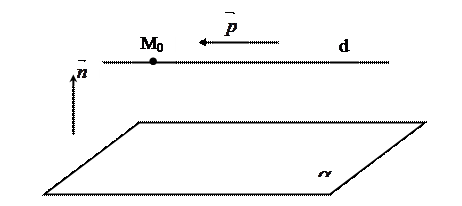
Рис. 18

3) Прямая лежит в плоскости, то есть: d 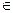α. В этом случае прямая и плоскость имеют бесчисленное множество общих точек.

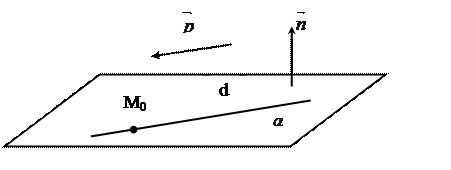
Рис. 19

Таким образом, задача о взаимном расположении прямой и плоскости сводится к вопросу о существовании общих точек, принадлежащих как прямой, так и плоскости. Это значит, что координаты этих точек должны удовлетворять как уравнению плоскости, так и уравнениям прямой, то есть являться решением системы уравнений:

.

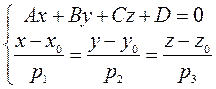Для решения этой системы уравнений относительно трёх неизвестных х,у и z, запишем её в виде:

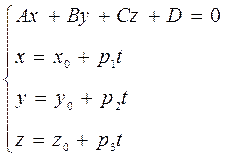
Для решения полученной системы четырёх уравнений относительно четырёх уравнений, сведём её к одному уравнению относительно одной переменной t. Для этого выражения для x, y и z последних уравнений подставим в первое уравнение. Таким образом получаем уравнение для определения параметра t, соответствующего точки пересечения прямой d и плоскости a: 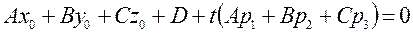(22)

Уравнение(21) имеет единственное решение, если

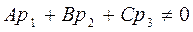(23)