Выясним, каков геометрический смысл условий (22), (23) и (24).
1) Условие (23): 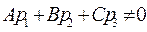 означает, что скалярное произведение направляющего вектора
означает, что скалярное произведение направляющего вектора 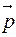 и вектора нормали
и вектора нормали 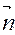 отличен от нуля, что означает что направляющий вектор прямой не параллелен α.
отличен от нуля, что означает что направляющий вектор прямой не параллелен α.
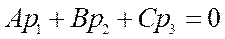 и и
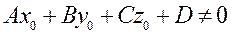
|
2) В условии (24):
первое соотношение означает, что скалярное произведение направляющего вектора прямой 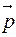 и вектора нормали
и вектора нормали 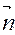 равно нулю => направляющий вектор прямой параллелен плоскости α. Второе соотношение означает, что точка М0(x0,y0,z0) не принадлежит плоскости α.
равно нулю => направляющий вектор прямой параллелен плоскости α. Второе соотношение означает, что точка М0(x0,y0,z0) не принадлежит плоскости α.
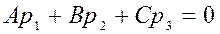 и и
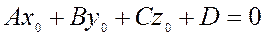
|
3) В условии (25):
первое соотношение означает, что скалярное произведение направляющего вектора прямой 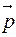 и вектора нормали
и вектора нормали 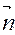 равно нулю => направляющий вектор прямой параллелен плоскости α. Второе соотношение означает, что точка М0(x0,y0,z0) принадлежит плоскости α.
равно нулю => направляющий вектор прямой параллелен плоскости α. Второе соотношение означает, что точка М0(x0,y0,z0) принадлежит плоскости α.
Пример.
Определить каково расположение прямой и плоскости, заданных  в аффинной системе координат уравнениями:
в аффинной системе координат уравнениями: 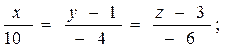
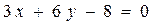 .
.
Решение
Находим координаты 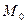 (0;-1;3) и
(0;-1;3) и 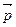 (10;-4;-6). Проверяем условие (22) Имеем
(10;-4;-6). Проверяем условие (22) Имеем 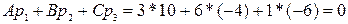 .
.  => Прямая или параллельна плоскости, или принадлежит плоскости. Проверяем второе условие параллельности прямой плоскости
=> Прямая или параллельна плоскости, или принадлежит плоскости. Проверяем второе условие параллельности прямой плоскости 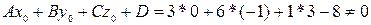 . => Прямая параллельна плоскости.
. => Прямая параллельна плоскости.
 2015-07-04
2015-07-04 1543
1543
