| Деятельность учителя | Деятельность учеников | Результативность |
| Предлагает учащимся решить ряд задач. | Выполняют предложенные задания. | Установление уровня успешности прохождения этапа практического применения знаний. |
Задача 1. Пусть в сосуде находится жидкость плотность 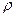 . Требуется найти разность давлений между двумя точками
. Требуется найти разность давлений между двумя точками 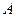 и
и 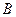 , находящимися на одной вертикали, если расстояние между этими точками равно
, находящимися на одной вертикали, если расстояние между этими точками равно 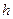 .
.
Дано: Решение:
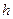
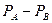 ─?
─?
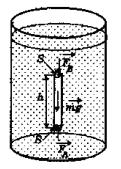
Рис.1
Мысленно выделим в жидкости тонкий вертикальный цилиндр, такой, что ось цилиндра проходит через точки 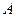 и
и 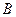 , и пусть точка
, и пусть точка 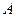 лежит на нижнем основании, а точка
лежит на нижнем основании, а точка 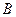 ─ на верхнем основании цилиндра. Пусть площадь основания цилиндра равна
─ на верхнем основании цилиндра. Пусть площадь основания цилиндра равна 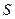 .
.
Рассмотрим все силы, действующие на наш воображаемый цилиндр в вертикальном направлении. На верхнее основание со стороны жидкости действует сила давления 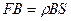 , а на нижнее основание - сила давления
, а на нижнее основание - сила давления 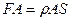 . Кроме того, на цилиндр действует еще одна сила - сила тяжести цилиндра
. Кроме того, на цилиндр действует еще одна сила - сила тяжести цилиндра 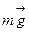 . Силы
. Силы 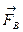 и
и 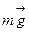 направлены вниз, а сила
направлены вниз, а сила 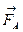 вверх. Так как вся жидкость, а значит, и наш цилиндр неподвижны, то равнодействующая сил, действующих на цилиндр в вертикальном направлении, равна нулю. Следовательно, сумма величин сил, направленных вниз,
вверх. Так как вся жидкость, а значит, и наш цилиндр неподвижны, то равнодействующая сил, действующих на цилиндр в вертикальном направлении, равна нулю. Следовательно, сумма величин сил, направленных вниз, 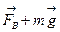 F равна величине силы, направленной вверх
F равна величине силы, направленной вверх 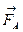 :
:
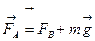 (1)
(1)
Масса цилиндра равна: 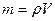 , где
, где 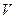 ─ объем цилиндра, а объем цилиндра,
─ объем цилиндра, а объем цилиндра, 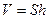 . Отсюда:
. Отсюда: 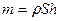 . Подставляя значения
. Подставляя значения 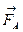 ,
, 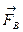 и
и 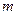 в равенство (1), получим:
в равенство (1), получим:
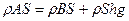 . Вынесем в правой части
. Вынесем в правой части 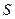 за скобки:
за скобки: 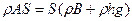 и разделим обе части последнего равенства на
и разделим обе части последнего равенства на 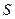 , получим:
, получим: 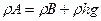 отсюда:
отсюда: 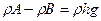
Задача решена. Заметим, что если точку 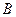 взять на поверхности жидкости, то давление жидкости в этой точке будет равно нулю:
взять на поверхности жидкости, то давление жидкости в этой точке будет равно нулю: 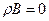 , а величина
, а величина 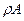 будет равна величине давления жидкости на глубине
будет равна величине давления жидкости на глубине 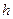 :
:
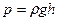 .
.
Формула позволяет рассчитывать гидростатическое давление в жидкости на глубине 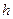 . Заметим, что это давление зависит только от плотности жидкости
. Заметим, что это давление зависит только от плотности жидкости 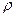 , напряженности гравитационного поля
, напряженности гравитационного поля 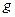 и глубины
и глубины 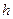 . От формы сосуда, в который налита жидкость, гидростатическое давление никак не зависит.
. От формы сосуда, в который налита жидкость, гидростатическое давление никак не зависит.
Задача 2. Определите давление жидкости на дно сосуда, показанного на рисунке. Плотность жидкости равна 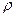 . Все размеры указаны на рисунке.
. Все размеры указаны на рисунке.
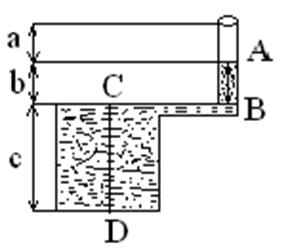
Рис 2
Решение
Проведем вертикальные отрезки 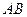 и
и 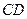 и горизонтальный отрезок
и горизонтальный отрезок 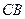 . Наша задача ─ найти давление на дне, то есть в точке
. Наша задача ─ найти давление на дне, то есть в точке 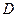 . Сначала найдем давление в точке
. Сначала найдем давление в точке 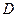 :
: 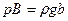 . Так как точки
. Так как точки 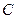 и
и 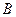 находятся на одной горизонтали, то давления в этих точках равны:
находятся на одной горизонтали, то давления в этих точках равны:
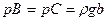 .
.
Теперь рассмотрим вертикальный отрезок 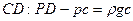
Отсюда 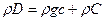 .
.
Подставим в последнюю формулу значение 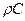 , получим:
, получим: 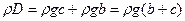
Следовательно, в качестве глубины действительно надо брать величину: 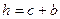
Индивидуальные задания (задания по рядам класса)
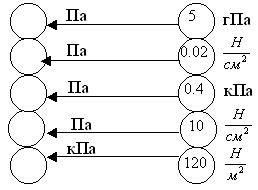
1. Задание на перевод единиц.
Переведите единицы давления и запишите в пустые кружки ответы.
2. Экспериментальное задание
Определите давление на дно стакана. Для этого измерьте высоту столба жидкости линейкой. Переведите сантиметры в метры.
Оставшиеся учащиеся решают задачи, предложенные учителем
Задание 1. В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте.
Дано: Решение:
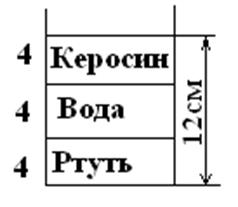
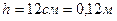
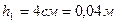
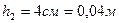
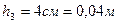
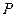 ─?
─?
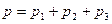
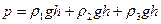
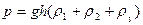
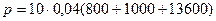
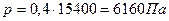
Ответ: 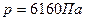
Задание 2. Прямоугольный сосуд вместимостью 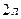 наполовину наполнен водой, а наполовину керосином, а) Каково давление жидкостей на дно сосуда?
наполовину наполнен водой, а наполовину керосином, а) Каково давление жидкостей на дно сосуда?
б) Чему равен вес жидкостей в сосуде? Дно сосуда имеет форму квадрата со стороной 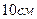 .
.
Дано: Решение:
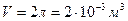
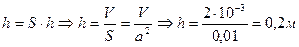
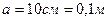
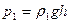 ,
, 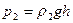
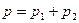
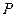 ─?
─? 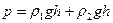
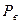 ─?
─? 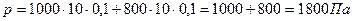
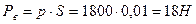
Ответ: 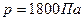 ,
, 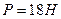
 2015-07-03
2015-07-03 990
990








