Доказательство

Для доказательства введем в рассмотрение на 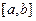следующую вспомогательную функцию:

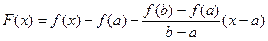, про которую можно сказать, что:

1) F (x) непрерывна на отрезке 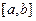как разность двух непрерывных функций f (x) и ,

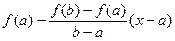2) F (x) дифференцируема на интервале : ,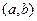

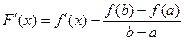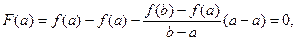
3) 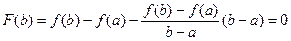, т.е. F (a) = F (b)

Вывод: функция y = F (x) удовлетворяет всем трем условиям теоремы Ролля, следовательно, существует точка 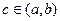такая, что 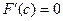, т.е.

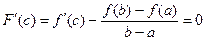, отсюда следует утверждение теоремы, что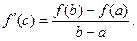

(что и требовалось доказать)

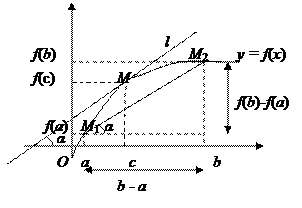Замечания.

1. Величина 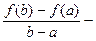угловой коэффициент секущей (М ₁, М ₂), проходящей через точки M ₁(a, f (a)) и M ₂(b, f (b)) к кривой ,

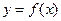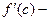угловой коэффициент касательной l к графику функции 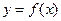в точке M (с, f (с)),

а так как 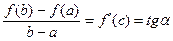, то обязательно существует точка 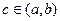такая, что касательная l к кривой в точке M (с, f (с)) параллельна секущей (М ₁, М ₂).

Таких точек с может быть несколько, но, по крайней мере, одна существует.

2. Равенство 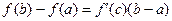называется формулой конечных приращений Лагранжа.