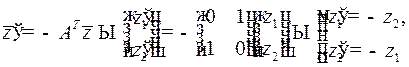
имеет общее решение
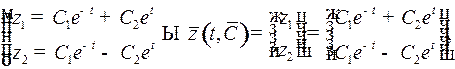 где
где 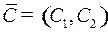 – постоянный вектор. Функция Понтрягина имеет вид
– постоянный вектор. Функция Понтрягина имеет вид
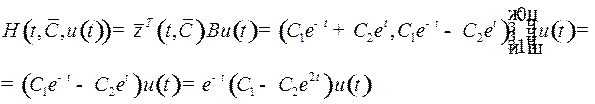
При фиксированном 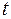 , если
, если 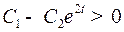 или
или 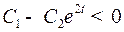 , то функция Понтрягина имеет максимальное значение, если взять
, то функция Понтрягина имеет максимальное значение, если взять 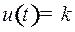 или
или 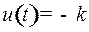 соответственно. Таким образом, функция управления
соответственно. Таким образом, функция управления 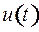 , доставляющая максимум функции Понтрягина, имеет только два значения
, доставляющая максимум функции Понтрягина, имеет только два значения 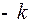 и
и 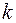 , и переключение этих значений происходит в единственной точке
, и переключение этих значений происходит в единственной точке 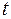 , в которой
, в которой 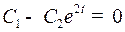 .
.
При таком выборе функции 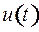 будет автоматически
будет автоматически 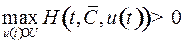 при всех
при всех 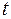 , кроме упомянутого исключительного значения.
, кроме упомянутого исключительного значения.
Найдем фазовые траектории под управлениями 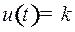 и
и 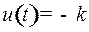 .
.
При 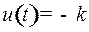 система (1) имеет вид
система (1) имеет вид
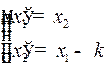 (2)
(2)
Ее общее решение
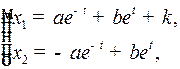 (3)
(3)
где 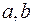 – произвольные постоянные. Исключив отсюда
– произвольные постоянные. Исключив отсюда 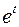 , получим
, получим
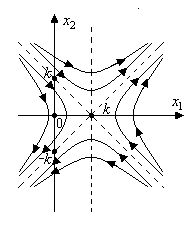
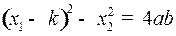 – семейство равнобочных гипербол с центром – семейство равнобочных гипербол с центром 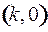 и асимптотами и асимптотами 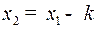 и и 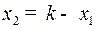 . Из равенства . Из равенства 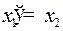 (в системе (2)) видно, что если (в системе (2)) видно, что если 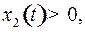 то то 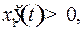 а если а если 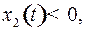 то то 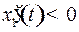 . Это значит, что с возрастанием времени . Это значит, что с возрастанием времени 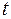 в верхней полуплоскости (где в верхней полуплоскости (где 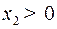 ) движение происходит слева направо ( ) движение происходит слева направо (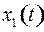 возрастает), а в нижней полуплоскости ( возрастает), а в нижней полуплоскости (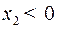 ) движение справа налево ( ) движение справа налево (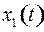 убывает). убывает).
| 
|
Аналогично при 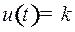 из системы
из системы 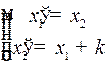 получаем
получаем
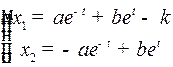 (4)
(4)
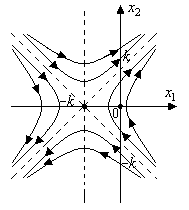
семейство равнобочных гипербол
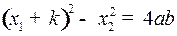 с центром с центром 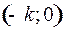 и с асимптотами и с асимптотами 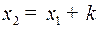 и и 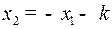 . Как и в случае . Как и в случае 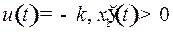 при при 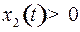 и и 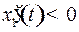 при при 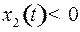 : в верхней полуплоскости движение происходит слева направо, в нижней полуплоскости – справа налево. : в верхней полуплоскости движение происходит слева направо, в нижней полуплоскости – справа налево.
| 
|
Движение фазовой точки 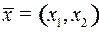 к пункту назначения
к пункту назначения 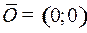 происходит слева направо по верхней части левой ветви гиперболы семейства (3) с уравнением
происходит слева направо по верхней части левой ветви гиперболы семейства (3) с уравнением
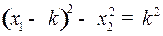 (5)
(5)
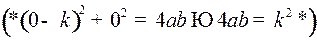 и справа налево по нижней части правой ветви гиперболы семейства (4) с уравнением
и справа налево по нижней части правой ветви гиперболы семейства (4) с уравнением
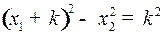 . (6)
. (6)
Линия переключения имеет уравнения
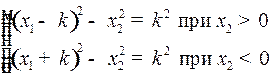 (7)
(7)
 2015-07-04
2015-07-04 407
407








