Как и в п. 2.5, оптимальная траектория будет состоять из куска одной из гипербол семейства (3) и (4) и куска линии переключения. Из рисунка видно, что если точка 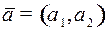 находится в полосе между прямыми
находится в полосе между прямыми 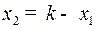 и
и 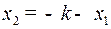 , то оптимальная траектория
, то оптимальная траектория
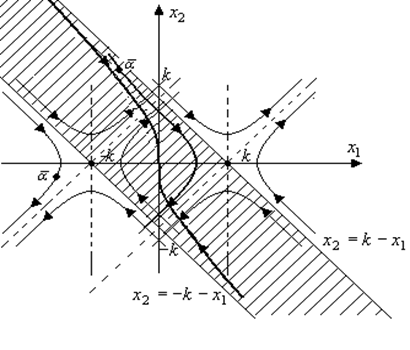
| найдется. Если же точка находится вне этой полосы или на одной из прямых 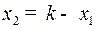 , , 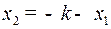 , то оптимальной траектории нет (Это объясняется тем, что в задаче имеется фазовое ограничение , то оптимальной траектории нет (Это объясняется тем, что в задаче имеется фазовое ограничение 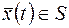 , так что , так что 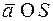 ). ).
|
Пусть, например, точка 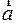 содержится в этой полосе левее линии переключения в верхней полуплоскости.
содержится в этой полосе левее линии переключения в верхней полуплоскости.
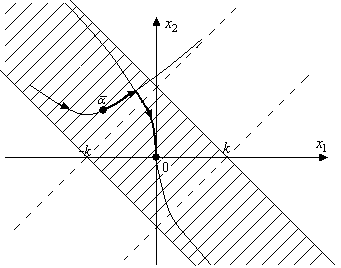
| Тогда по одной из гипербол семейства (4) под управлением 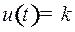 в некоторый момент в некоторый момент 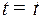 дойдем до линии переключения и затем по линии переключения под управлением дойдем до линии переключения и затем по линии переключения под управлением 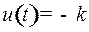 дойдем до точки дойдем до точки 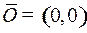 . Эта траектория будет оптимальной, так как выполняется принцип максимума Понтрягина. . Эта траектория будет оптимальной, так как выполняется принцип максимума Понтрягина.
|
Действительно, при 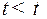 , т.е.
, т.е. 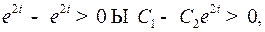 где
где 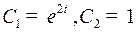 , использовано управление
, использовано управление  , а при
, а при 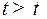 , т.е.
, т.е. 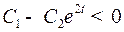 , использовано управление
, использовано управление 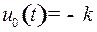 . Это значит, что при постоянном векторе
. Это значит, что при постоянном векторе 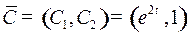 при всех
при всех 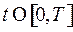 (кроме
(кроме 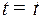 ) управление
) управление 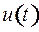 выбрано так, что функция Понтрягина
выбрано так, что функция Понтрягина 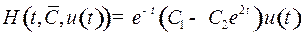 имеет максимальное значение – выполняется п.1) принципа максимума Понтрягина. Как было отмечено раньше, п.2) выполняется автоматически:
имеет максимальное значение – выполняется п.1) принципа максимума Понтрягина. Как было отмечено раньше, п.2) выполняется автоматически:
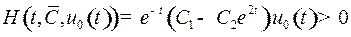 .
.
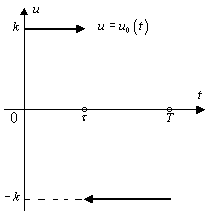
| Оптимальное управление имеет вид
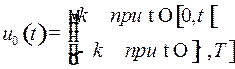 .
Аналогично определяются оптимальное управление и оптимальная траектория при других расположениях точки .
Аналогично определяются оптимальное управление и оптимальная траектория при других расположениях точки 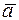 относительно линии переключения. относительно линии переключения.
|
 2015-07-04
2015-07-04 280
280








