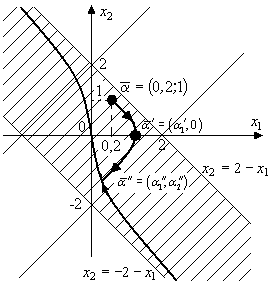
| 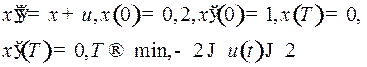 (в момент (в момент 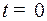 маятник отклонен от положения равновесия на угол 0,2 радиан и движется влево со скоростью 1 ед.). Здесь маятник отклонен от положения равновесия на угол 0,2 радиан и движется влево со скоростью 1 ед.). Здесь 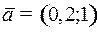 . Можно убедиться, что точка . Можно убедиться, что точка 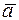 содержится в полосе управляемости между прямыми содержится в полосе управляемости между прямыми 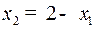 и и 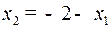 , правее линии переключения в верхней полуплоскости. , правее линии переключения в верхней полуплоскости.
|
□ До линии переключения дойдем по гиперболе семейства (3), проходящей через эту точку, под управлением 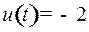 . Найдем закон движения по такой гиперболе с момента
. Найдем закон движения по такой гиперболе с момента 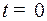 из точки
из точки 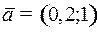 :
:
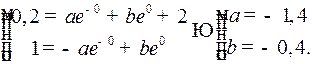
Закон движения имеет вид:
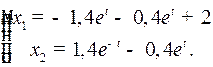
Гипербола имеет уравнение:
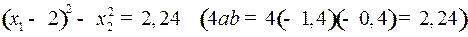 .
.
Найдем точку её пересечения с линией переключения (7) (у нас 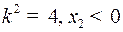 )
)
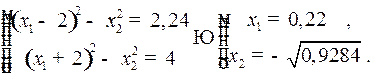
Найдем момент 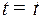 попадания в эту точку:
попадания в эту точку:
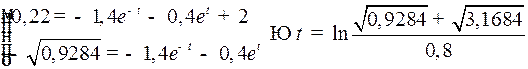 .
.
Теперь найдем закон движения из точки 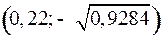 с момента
с момента 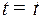 по линии переключения – гиперболе семейства (4):
по линии переключения – гиперболе семейства (4):
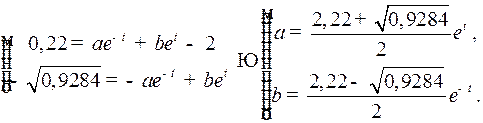
Закон движения имеет вид:
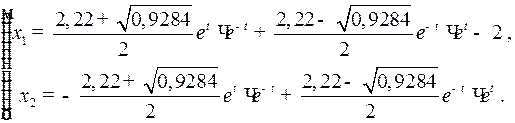
Найдем момент 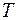 попадания в точку назначения
попадания в точку назначения 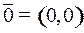 (достаточно воспользоваться вторым равенством):
(достаточно воспользоваться вторым равенством):
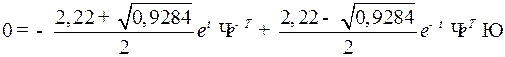
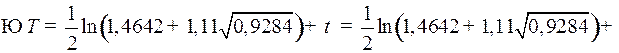
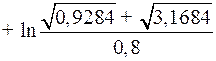 .
.
Итак, оптимальная траектория имеет вид:
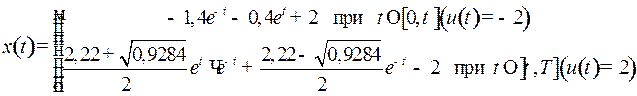 где
где 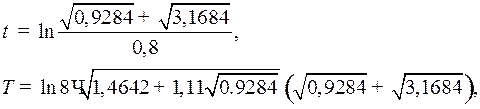
оптимальное управление 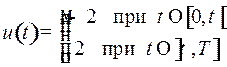
Судя по фазовой траектории на последнем рисунке, управление движением маятника происходит так:
В момент 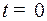 , когда включили управление, маятник был отклонен от положения равновесия на угол 0,2 радиан влево и продолжал отклоняться влево со скоростью 1 ед. Чтобы замедлить и остановить его отклонение влево, включили двигатель на полную мощность
, когда включили управление, маятник был отклонен от положения равновесия на угол 0,2 радиан влево и продолжал отклоняться влево со скоростью 1 ед. Чтобы замедлить и остановить его отклонение влево, включили двигатель на полную мощность 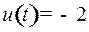 в направлении вправо. Маятник был остановлен (скорость
в направлении вправо. Маятник был остановлен (скорость 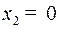 ) при некотором положительном отклонении
) при некотором положительном отклонении 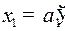 (слева от положения равновесия). Это – фазовое состояние
(слева от положения равновесия). Это – фазовое состояние 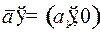 . Под тем же управлением
. Под тем же управлением 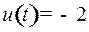 маятник стал приближаться назад к положению равновесия (уже с отрицательной скоростью
маятник стал приближаться назад к положению равновесия (уже с отрицательной скоростью 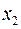 ). Чтобы маятник не перескочил через положение равновесия, в момент
). Чтобы маятник не перескочил через положение равновесия, в момент 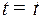 управление было переключено на
управление было переключено на 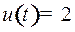 (для замедления маятника). Это – фазовое состояние
(для замедления маятника). Это – фазовое состояние 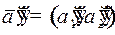 . После этого маятник пришел в положение равновесия со скоростью
. После этого маятник пришел в положение равновесия со скоростью 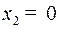 (в момент
(в момент 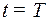 ). ■
). ■
Контрольные вопросы
1. С помощью критерия Калмана проверить управляемость системы
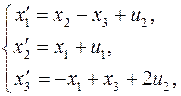
где 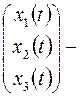 фазовый вектор,
фазовый вектор, 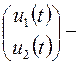 вектор управления.
вектор управления.
2. Составить сопряженную систему для однородной линейной системы дифференциальных уравнений с постоянными коэффициентами
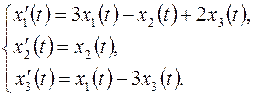
3. Найти общее решение сопряженной системы для однородной линейной системы дифференциальных уравнений с постоянными коэффициентами
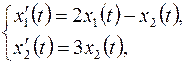
4. Написать функцию Понтрягина к задаче
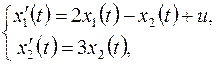
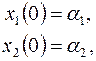
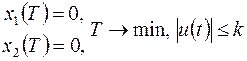 ,
,
где 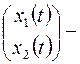 фазовый вектор,
фазовый вектор, 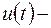 управление,
управление, 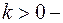 постоянная.
постоянная.
 2015-07-04
2015-07-04 262
262







