2015-07-21
315
Допустим, тип эмпирической формулы выбран, и ее можно представить в виде
,
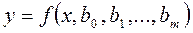где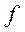 
– известная функция; 
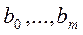– неизвестные постоянные параметры.
Задача заключается в том, чтобы определить такие значения этих параметров, при которых эмпирическая формула дает хорошее приближение данной функции, значения которой в опытных точках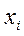 
равны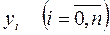 
.
Разность между значениями опытных данных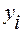 
и расчётными значениями по эмпирической формуле в точках 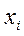обозначим через 
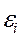, т.е.:
, 
.
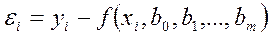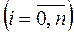Задача нахождения наилучших значений параметров: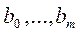 
, сводится к некоторой минимизации отклонений 
.
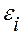Существует несколько способов решения этой задачи. Рассмотрим определение наилучших значений параметров методом наименьших квадратов.
