Рассмотрим применение метода наименьших квадратов для случая, широко используемого на практике, когда в качестве эмпирической формулы используется многочлен вида:
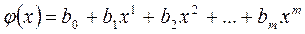 . (22)
. (22)
Формула (18) для определения суммы квадратов отклонений S для этого случая будет иметь вид
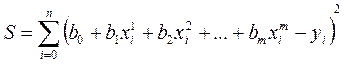 . (23)
. (23)
Для составления системы уравнений (19) найдем и приравняем нулю частные производные функции 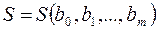 :
:
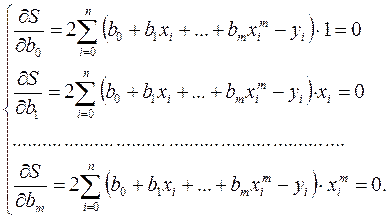 . (24)
. (24)
Собирая коэффициенты при неизвестных 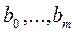 , получаем следующую систему нормальных уравнений:
, получаем следующую систему нормальных уравнений:
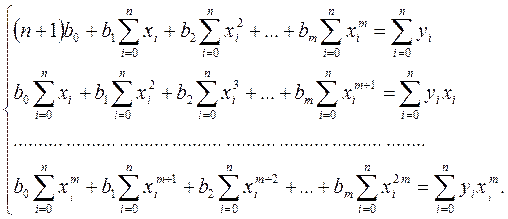 (25)
(25)
Решая эту систему линейных уравнений, получим коэффициенты 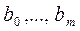 многочлена, которые являются искомыми наилучшими параметрами эмпирической формулы (22).
многочлена, которые являются искомыми наилучшими параметрами эмпирической формулы (22).
Из рассмотренного случая вытекает частный случай линейной эмпирической формулы от одного параметра
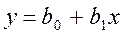 . (27)
. (27)
Для выборки объемом (n +1) система нормальных уравнений при этом имеет вид:
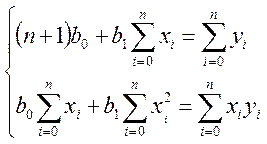 (28)
(28)
Коэффициенты 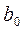 и
и 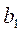 можно найти с помощью определителей (по правилу Крамера):
можно найти с помощью определителей (по правилу Крамера):
 , (29)
, (29)
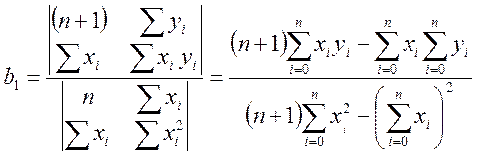 . (30)
. (30)
 2015-07-21
2015-07-21 454
454







