2.1. Задача интерполирования
1) Математический смысл и геометрическая интерпретация задачи интерполирования
Аппроксимирующую функцию Q можно искать в виде полинома степени m:
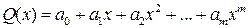 .
.
Если при этом предположить, что экспериментальные значения 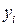 в таблице не имеют погрешности, то естественно принять в качестве критерия близости f (x) и Q (x) равенство их значений в точках
в таблице не имеют погрешности, то естественно принять в качестве критерия близости f (x) и Q (x) равенство их значений в точках 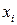 , т.е.
, т.е.
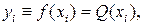
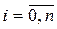 .
.
Такая задача называется задачей интерполирования, а точки 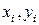 – узлами интерполяции. Многочлен Q (x) называется интерполяционным многочленом.
– узлами интерполяции. Многочлен Q (x) называется интерполяционным многочленом.
2) Интерполяционный многочлен Лагранжа
а) Определение коэффициентов интерполяционного многочлена канонического вида из решенияСЛУ
Задача заключается в том, чтобы построить интерполяционный многочлен единый для всего интервала 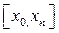 . Запишем исходный многочлен в каноническом виде:
. Запишем исходный многочлен в каноническом виде: 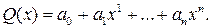
Он единственен, т. к. степень его на единицу меньше числа узлов (n +1).
Из условий равенства значений этого многочлена в узлах 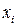 соответствующим заданным табличным значениям
соответствующим заданным табличным значениям 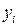 путем подстановки в полином значений
путем подстановки в полином значений 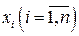 и приравнивания значений полинома эмпирическим данным
и приравнивания значений полинома эмпирическим данным 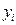 , получим следующую систему линейных уравнений (СЛУ) для нахождения его коэффициентов
, получим следующую систему линейных уравнений (СЛУ) для нахождения его коэффициентов 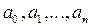 :
:
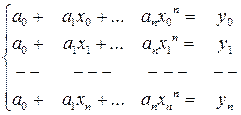 .
.
Эта система уравнений, включает (n +1) уравнение с (n +1) неизвестными коэффициентами 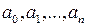 и имеет единственное решение, если среди узлов интерполяции нет совпадающих:
и имеет единственное решение, если среди узлов интерполяции нет совпадающих: 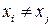 при
при 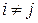 .
.
б) Интерполяционный многочлен Лагранжа
Многочлен Лагранжа имеет вид
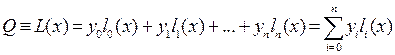 , (1)
, (1)
где 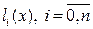 – многочлены степени n, удовлетворяющие условиям:
– многочлены степени n, удовлетворяющие условиям:
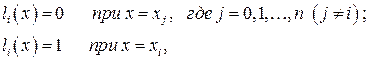
т.е. каждый многочлен 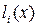 обращается в нуль во всех узлах
обращается в нуль во всех узлах 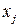
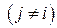 интерполяции за исключением одного i -го, где он равняется единице.
интерполяции за исключением одного i -го, где он равняется единице.
Этим условиям отвечают, например, многочлены вида:
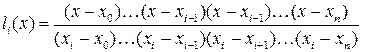 (2)
(2)
Подставляя (2) в (1), получим
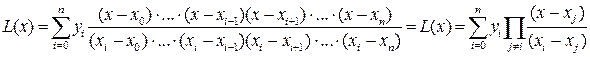 . (3)
. (3)
Формула (3) называется интерполяционным многочленом Лагранжа.
Докажем, что этот многочлен является единственным. Допустим противоположное. Пусть существует ещё один многочлен F (x) степени n, принимающий в узлах интерполяции заданные значения, т.е. 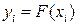 . Тогда разность
. Тогда разность 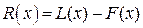 , являющаяся многочленом степени n (или ниже), в узлах
, являющаяся многочленом степени n (или ниже), в узлах 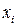 равна
равна
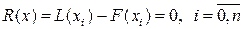 .
.
Это означает, что многочлен R (x) степени не больше n имеет (n +1) корней, что невозможно. Отсюда следует, что 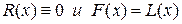 .
.
Остается рассмотреть вопрос с точностью аппроксимации функции f (x), полиномом 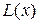 в других точках (отличных от узлов интерполяции), которая определяется остаточным членом
в других точках (отличных от узлов интерполяции), которая определяется остаточным членом 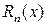 :
:
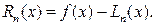 |
Если y = f (x) в рассматриваемой области изменения 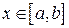 , содержащей узлы интерполирования, имеет все производные до (n +1) -го порядка:
, содержащей узлы интерполирования, имеет все производные до (n +1) -го порядка:
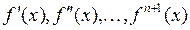 ,
,
то точность приближения оценивается следующим соотношением:
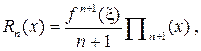 | |||
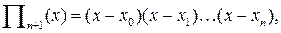 |
где а x зависит от x
и лежит внутри отрезка [ a, b ].
Если обозначить 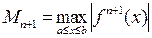 , то получим следующую оценку для абсолютной погрешности интерполяционной формулы Лагранжа:
, то получим следующую оценку для абсолютной погрешности интерполяционной формулы Лагранжа:
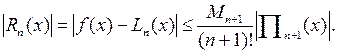 |
 2015-07-21
2015-07-21 1484
1484








