Если 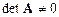 , то существует матрица
, то существует матрица 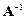 , обратная к данной. Умножим исходную систему уравнений (2.1) на обратную матрицу слева. Получим
, обратная к данной. Умножим исходную систему уравнений (2.1) на обратную матрицу слева. Получим
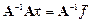 .
.
Известно, что произведение обратной матрицы на исходную дает единичную матрицу 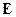 , и, следовательно, получаем
, и, следовательно, получаем 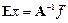 , или
, или
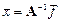 (2.3)
(2.3)
Решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция. Однако для небольших m решение может быть получено с помощью функций Excel.
ПРИМЕР 2.3. С помощью метода обратной матрицы решить систему 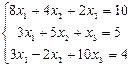
Занесем на рабочий лист Excel матрицу коэффициентов
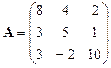 и вектор правых частей
и вектор правых частей 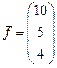 .
.
Выделим на рабочем листе область размером  ячейки для обратной матрицы и вызовем функцию МОБР. В поле Массив занесем адреса ячеек исходной матрицы A, и, нажав комбинацию клавиш Ctrl+Shift+Enter, получим A-1:
ячейки для обратной матрицы и вызовем функцию МОБР. В поле Массив занесем адреса ячеек исходной матрицы A, и, нажав комбинацию клавиш Ctrl+Shift+Enter, получим A-1:
| 0.195489 | -0.16541 | -0.02256 |
| -0.1015 | 0.278195 | -0.00752 |
| -0.07895 | 0.105263 | 0.105263 |
Полученную обратную матрицу умножим на вектор правых частей 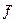 . Для этого выделим столбец из трех ячеек и вызовем функцию МУМНОЖ. В поля Массив 1 и Массив 2 занесем адреса ячеек, в которых находятся найденная обратная матрица и вектор правых частей, после чего, нажав комбинацию клавиш Ctrl+Shift+Enter, получим решение СЛАУ
. Для этого выделим столбец из трех ячеек и вызовем функцию МУМНОЖ. В поля Массив 1 и Массив 2 занесем адреса ячеек, в которых находятся найденная обратная матрица и вектор правых частей, после чего, нажав комбинацию клавиш Ctrl+Shift+Enter, получим решение СЛАУ
| 1.037594 |
| 0.345865 |
| 0.157895 |
Замечание. Если одна из клавиш Ctrl или Shift не нажата, вычисления будут выполнены не во всем выделенном диапазоне, а только в одной ячейке. В этом случае весь процесс вызова функции необходимо повторить.
 2015-07-21
2015-07-21 614
614








