Метод Крамера

Метод Крамера относится к классу точных методов решения СЛАУ. На практике он часто используется при небольшой размерности системы 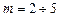. Формулы метода Крамера решения СЛАУ выглядят как:

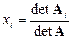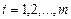, () (2.2)

Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц 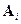, получаемых из 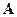заменой i -го столбца столбцом правых частей. Так матрица 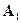получается из матрицы 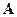заменой первого столбца на столбец правых частей .

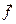Размерность системы (т.е. число неизвестных 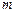) является главным фактором, из-за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с 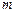неизвестными требует порядка 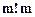арифметических операций. Таким образом, для решения системы, например, из 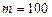уравнений потребуется совершить 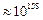операций, что не под силу даже самым мощным современным ЭВМ. Для небольших m решение можно найти с помощью функций Excel.

ПРИМЕР 2.1. Рассмотрим метод Крамера на примере системы двух линейных уравнений вида .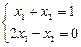
Найдем определители:

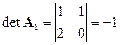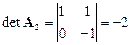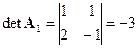, , . Решение по формулам Крамера: , .

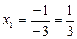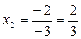ПРИМЕР 2.2. Решить методом Крамера СЛАУ

.

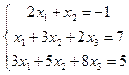Занесем на рабочий лист матрицу СЛАУ, вектор правых частей ,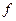

A = 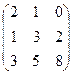, f = 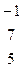, а также вспомогательные матрицы

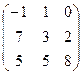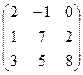A₁ = A₂ = A₃ = .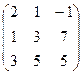

С помощью функции Excel МОПРЕД вычислим D = det A = 26, D₁ = det A₁ = ‑ 60, D₂ = det A₂ = 94, D₃ = det A₃ = ‑ 20. По формулам (2.2) находим x ₁ = D₁/D = ‑ 2.3077, x ₂ = D2/D = 3.6154, x ₃ = D₃/D = ‑ 0.7692.