Имеется набор узлов интерполяции 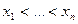 и значений функции
и значений функции  . Необходимо построить по этим данным интерполяционный многочлен
. Необходимо построить по этим данным интерполяционный многочлен 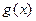 . Этот многочлен, исходя из (125) и (130) будет иметь степень
. Этот многочлен, исходя из (125) и (130) будет иметь степень 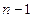 . Задача интерполирования будет решена, если удастся построить многочлены
. Задача интерполирования будет решена, если удастся построить многочлены 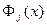 ,
, 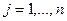 , степени
, степени 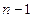 такие, что
такие, что
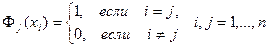 . (135)
. (135)
Тогда многочлен
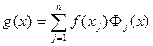 (140)
(140)
будет искомым интерполяционным многочленом. Действительно, поскольку 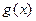 в соответствии с (140) – сумма многочленов степени
в соответствии с (140) – сумма многочленов степени 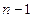 , то и
, то и 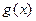 - многочлен степени
- многочлен степени 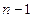 . Проверим выполнения условия интерполяции:
. Проверим выполнения условия интерполяции:
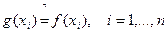 . (150)
. (150)
Вычислим
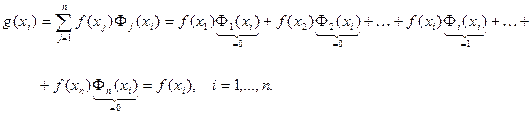
Таким образом, условие (150) выполнено.
Задание многочленов 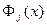 ,
, 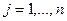 , в виде (135) определяет
, в виде (135) определяет 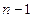 корень для каждого из
корень для каждого из 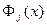 - это узлы интерполирования
- это узлы интерполирования 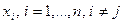 , для которых
, для которых 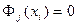 . Поскольку степень
. Поскольку степень 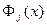 -
- 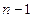 , то известны все корни
, то известны все корни 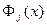 , и тогда имеет место представление:
, и тогда имеет место представление:
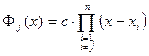 . (160)
. (160)
где 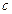 - пока неизвестная константа.
- пока неизвестная константа.
Поскольку при совпадении индексов 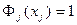 , то из (160) следует:
, то из (160) следует:
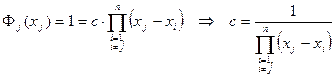 . (170)
. (170)
Тогда с учетом (170) 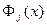 имеет вид:
имеет вид:
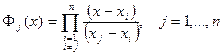 ,
,
а искомый интерполяционный многочлен 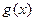 с учетом (140):
с учетом (140):
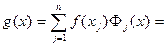
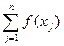
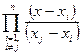 . (180)
. (180)
Многочлен (180) называется интерполяционным многочленом Лагранжа для функции 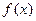 , построенным по набору
, построенным по набору 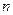 узлов интерполяции
узлов интерполяции 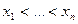 и часто обозначается:
и часто обозначается: 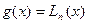 - здесь
- здесь 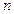 - это количество узлов интерполяции (соответственно степень многочлена Лагранжа будет на единицу меньше, т.е.
- это количество узлов интерполяции (соответственно степень многочлена Лагранжа будет на единицу меньше, т.е. 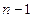 ).
).
Как можно оценить качество интерполянта? После того, как вычисленны коэффициенты 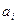 (представление (125)), следующий шаг – вычислить значение интерполянта в заданных узлах
(представление (125)), следующий шаг – вычислить значение интерполянта в заданных узлах 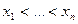 и проверить, что заданные значения функции
и проверить, что заданные значения функции  , в этих узлах воспроизводятся в пределах ошибок округления. На практике интерполянт будет вычисляться во многих других точках, и невозможно установить его общее поведение, зная только, что он хорошо воспроизводит входные данные. Но все-таки в некоторых ситуациях качество интерполянта можно проанализировать.
, в этих узлах воспроизводятся в пределах ошибок округления. На практике интерполянт будет вычисляться во многих других точках, и невозможно установить его общее поведение, зная только, что он хорошо воспроизводит входные данные. Но все-таки в некоторых ситуациях качество интерполянта можно проанализировать.
Обозначим
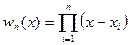 . (185)
. (185)
Можно доказать, что для любого 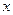 :
:
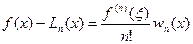 , (190)
, (190)
где 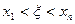 .
.
Действительно, предположим, что 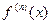 непрерывна на
непрерывна на 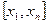 . Оценим разность
. Оценим разность 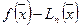 , где
, где 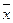 . Пусть
. Пусть
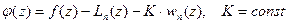 . (195)
. (195)
Выберем 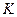 из условия
из условия
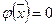 .
.
Очевидно:
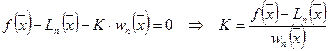 , (197)
, (197)
т.е. 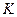 принципиально можно найти.
принципиально можно найти.
При т аком выборе 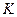 функция
функция 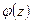 обращается в 0 в
обращается в 0 в 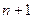 точке:
точке: 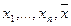 . На основании теоремы Ролля ее производная
. На основании теоремы Ролля ее производная 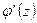 обращается в ноль, по крайней мере, в
обращается в ноль, по крайней мере, в 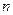 точках (т. Ролля: если функция
точках (т. Ролля: если функция 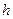 непрерывна на отрезке
непрерывна на отрезке 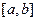 , дифференцируема в
, дифференцируема в 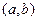 , и
, и 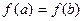 , то существует, по крайней мере, одна точка
, то существует, по крайней мере, одна точка 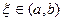 , что
, что 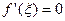 ).
).
Применяя теорему Ролля к функции 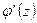 ,получаем, что ее производная
,получаем, что ее производная 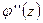 обращается в 0, по крайней мере, в
обращается в 0, по крайней мере, в 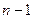 точке и т.д.. В итоге получаем, что
точке и т.д.. В итоге получаем, что 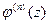 обращается в 0, по крайней мере, в одной точке
обращается в 0, по крайней мере, в одной точке 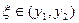 , где
, где 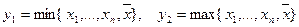 .
.
Поскольку
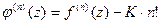
то
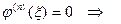
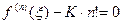 ,
,
а значит
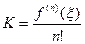 . (200)
. (200)
Поскольку из (197) 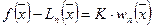 , то подставляя сюда
, то подставляя сюда 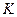 из (200), получим:
из (200), получим:
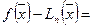
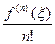
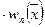 ,
, 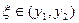 . (210)
. (210)
Формула (210) – формула остаточного члена (или погрешности) интерполяционного многочлена Лагранжа.
Пример. Вычислить погрешность (ошибку) полиномиальной интерполяции третьей степени для функции 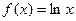 , построенную по узлам
, построенную по узлам 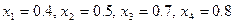 . Необходимо оценить ошибку интерполяции в точке
. Необходимо оценить ошибку интерполяции в точке 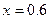 .
.
Интерполяционный многочлен Лагранжа 3-ей степени в соответствии с формулой (180) имеет вид
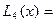
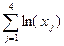
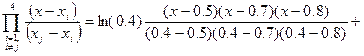
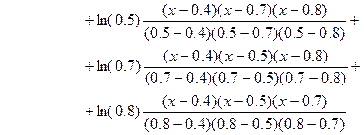
и 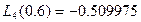 .
.
Выражение для погрешности дает в соответствии с (190) дает:
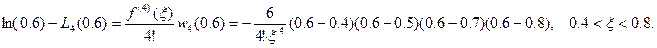
Таким образом, ошибка будет меньше, чем
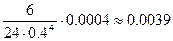 . (220)
. (220)
Фактическая величина погрешности есть
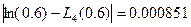 ,
,
что полностью соответствует оценке (220).
Рассмотрим, что получится, если интерполировать известную функцию 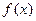 все в большем и большем числе точек на фиксированном интервале. Логично, на первый взгляд надеется, что оценка погрешности интерполяции в точках, отличных от узлов, улучшится. Однако, если внимательно посмотреть на выражение (210) для погрешности интерполяции, то можно заметить следующее: хотя факториал и произведение разностей с увеличением
все в большем и большем числе точек на фиксированном интервале. Логично, на первый взгляд надеется, что оценка погрешности интерполяции в точках, отличных от узлов, улучшится. Однако, если внимательно посмотреть на выражение (210) для погрешности интерполяции, то можно заметить следующее: хотя факториал и произведение разностей с увеличением 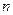 уменьшают ошибку, но при этом растет порядок производной
уменьшают ошибку, но при этом растет порядок производной 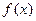 . Для большинства функций величины производных увеличиваются быстрее, чем
. Для большинства функций величины производных увеличиваются быстрее, чем 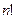 . В результате полиномиальные интерполянты редко сходятся к обычной непрерывной функции
. В результате полиномиальные интерполянты редко сходятся к обычной непрерывной функции 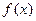 с ростом
с ростом 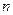 . Практический эффект выражается в том, что полиномиальный интерполянт высокой степени может «вести себя плохо», приближая значения
. Практический эффект выражается в том, что полиномиальный интерполянт высокой степени может «вести себя плохо», приближая значения 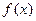 в точках, отличных от узлов интерполяции. Поэтому почти всегда используются интерполянты степени не выше 4 или 5.
в точках, отличных от узлов интерполяции. Поэтому почти всегда используются интерполянты степени не выше 4 или 5.
Пример. Функция Рунге.
Подробный анализ опасностей, возникающих при полиномиальной интерполяции, был впервые опубликован Рунге в 1901 г. Он пытался интерполировать полиномами простую функцию
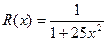
в точках равномерной сетки на сегменте 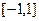 . Он обнаружил, что при стремлении степени
. Он обнаружил, что при стремлении степени 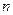 интерполирующего полинома
интерполирующего полинома 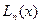 к бесконечности
к бесконечности 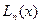 не стремятся к
не стремятся к 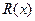 при
при 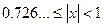 . Это явление графически показано на рис.3. При этом полиномиальная интерполяция хорошо работает в средней части
. Это явление графически показано на рис.3. При этом полиномиальная интерполяция хорошо работает в средней части 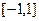 .
.
Расходимость последовательности интерполянтов 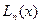 с ростом
с ростом 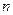 объясняется быстрым ростом производных
объясняется быстрым ростом производных 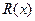 с ростом их порядка
с ростом их порядка 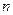 (см.(210)).
(см.(210)).
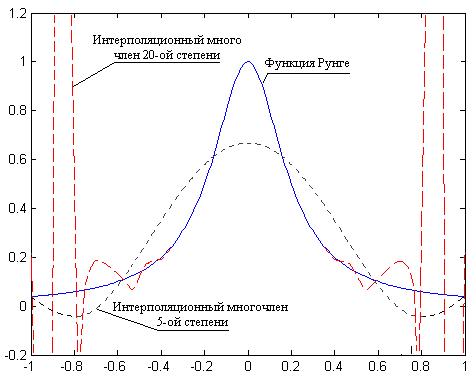
Рис.3.
Замечание 1. Если узлы интерполирования расположить неравномерно, сконцентрировав их ближе к концам 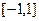 , то расходимость последовательности интерполянтов исчезнет. В результате полиномиальные интерполянты будут сходиться к
, то расходимость последовательности интерполянтов исчезнет. В результате полиномиальные интерполянты будут сходиться к 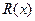 при стремлении
при стремлении 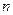 к бесконечности для любого
к бесконечности для любого 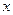 из
из 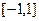 . Однако, в общем случае такой прием не срабатывает: не существует правила для выбора узлов интерполяции, которое бы работало для всех непрерывных функций. В то же время для любой конкретной функции
. Однако, в общем случае такой прием не срабатывает: не существует правила для выбора узлов интерполяции, которое бы работало для всех непрерывных функций. В то же время для любой конкретной функции 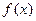 можно индивидуально подобрать расположение узлов.
можно индивидуально подобрать расположение узлов.
Замечание 2. Число арифметических операций для построения интерполяционного многочлена Лагранжа по 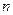 узлам интерполяции в соответствии с формулой (180) составляет
узлам интерполяции в соответствии с формулой (180) составляет 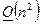 арифметических операций.
арифметических операций.
Замечание 3. Существует много обобщений для интерполяции Лагранжа. Например, интерполяции Эрмита. Исходными данными здесь являются значения приближаемой функции 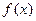 и значения ее производной в узлах интерполирования:
и значения ее производной в узлах интерполирования: 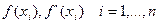 . Задача состоит в том, чтобы найти полином
. Задача состоит в том, чтобы найти полином 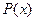 максимальной степени
максимальной степени 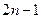 такой, что
такой, что
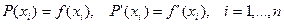 .
.
 2014-02-09
2014-02-09 3151
3151
