Законы распределения дискретной случайной величины

Законом распределения случайной величины называется соответствие между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения дискретной случайной величины может быть задан таблицей:

X	x1	x2	¼	xn
p	p1	p2	¼	pn

Таблица может быть и бесконечной.

p₁ = p(х = x₁), p₂ = p(х = x₂), ¼, p_n = p(х = x_n).

(где х - случайная величина, р – её вероятности).

1. Биномиальное распределение

Дискретная случайная величина X - число появлений события А в n повторных независимых испытаниях, причем для каждого испытания Р(А) = р, Р(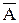) = 1 - p = q.

Вероятности значений случайной величины X равны:

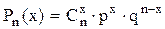, где 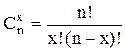(3.23)

Математическое ожидание числа событий А в n испытаниях будет равно: M(X) = np.

Дисперсия числа событий будет равна: D(X) = np×(1 - p) = npq.

Среднее квадратическое отклонение равно: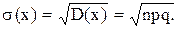

2. Распределение Пуассона

Дискретная случайная величина Х - число появлений события А в n повторных независимых испытаниях (n велико), причем для каждого испытания Р(А) = р, Р(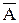) = 1 - p = q, р < 0,1.

Вероятности значений случайной величины Х равны

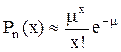, (3.24)

где m - параметр распределения

Распределение Пуассона может использоваться в качестве хорошего приближения биномиального распределения, если n велико и р мало. Тогда в качестве m нужно взять nр.

Математическое ожидание и дисперсия этой случайной величины равны: M(x) = m, D(x) = m.

Распределение Пуассона описывается одним параметром m.

3. Нормальное распределение (закон Гаусса)

Нормальный закон распределения играет огромную роль в медико- биологических наблюдениях и экспериментах. При действии большого числа случайных факторов, каждый из которых сам по себе оказывает независимо от других незначительное действие на случайную величину, последняя подчиняется нормальному закону.

Для нормального распределения, имеющего математическое ожидание m и среднее квадратическое отклонение s, плотность распределения имеет вид:

.

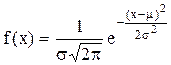Нормальное распределение с параметрами m = 0 и s = 1 называют нормированным, или стандартным. Функция плотности вероятности нормированного распределения:

.

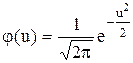Вероятность попадания нормально распределенной случайной величины в интервал [a, b] равна:

,

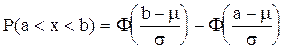где 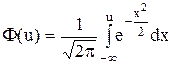- функция распределения нормированного нормального распределения Ф(u) + Ф(-u) = 1.