Характеристики дискретной случайной величины

Случайную величину часто удобно выражать числовыми характеристиками, к которым относятся: 1) среднее арифметическое значение, 2) математическое ожидание, 3) дисперсия и 4) среднее квадратичное отклонение.

1. Среднее арифметическое значение ДСВ: Х= ∑ х /n

2. Математическим ожиданием M(X) случайной величины X называют сумму произведений всех ее возможных значений на их вероятности: .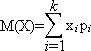

Это число представляет собой средний результат, который можно ожидать при большом количестве выполнений эксперимента. Таким образом, математическое ожидание есть сумма всех возможных значений случайной величины с весами, равными их вероятностям или математическое ожидание числа появлений события в одном испытании равно вероятности этого события. Вероятностный смысл математического ожидания состоит в том, что оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Свойства математического ожидания:

а) Математическое ожидание постоянной равно этой постоянной: M(C)= C

б) Постоянный множитель можно выносить за знак математического ожидания: M(CX) = C M(X)

в) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M(XY) = M(X) * M(Y)

г) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: M(X+Y) = M(X) + M(Y)

3. Дисперсия. Среднее значение квадрата отклонения называется дисперсией. В переводе с латинского "дисперсия" означает "рассеяние". Дисперсия служит характеристикой разброса значений случайной величины.

Дисперсией D(X) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: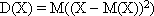

Существует и другая формула для вычисления дисперсии, по которой можно вычислить её значение намного быстрее: дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания: D(X) = M(X²) – (M(X))². Эта формула даётся без вывода.

Свойства дисперсии:

а) Дисперсия постоянной равна нулю: D(C)=0

б) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: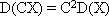

в) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X+Y)=D(X) + D(Y).

Это также относится к любому числу независимых случайных величин.

г) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X-Y) = D(X) + D(Y).

4. Среднее квадратическое отклонение служит для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения.

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии: .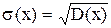

Дисперсия имеет размерность, равную квадрату размерности случайной величины. Например, если Х выражается в линейных метрах, то σ(Х) будет выражаться также в линейных метрах, а D(X) – в квадратных метрах.

Среднее квадратическое отклонение суммы конечного числа независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

σ (Х₁ +Х₂ +…+ Х_n ) = √ σ² (Х₁) + σ² (Х₂)+ … + σ² (Х_n)

Если несколько случайных величин имеют одинаковые распределения, то их числовые характеристики одинаковы.