Их вероятностный смысл

Непрерывная случайная величина может принимать любое из значений промежутка (а, b). При этом одно возможное значение этой случайной величины нельзя отделить от другого каким-либо промежутком, не содержащим ее значения. Т.е. непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Составить перечень всех возможных значений случайной величины Х нельзя, поэтому целесообразно задавать способы задания любых типов случайных величин.

Функцией распределения непрерывной случайной величины называют функцию F(х), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е. F (х) = Р(Х < х).

Геометрически это можно понять так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х. Можно сказать, что случайная величина Х называется непрерывной, если для любых a < b существует такая неотрицательная функция f (x), что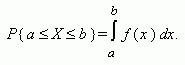

Свойства функции распределения

1. Значения функции распределения принадлежат отрезку [0,1]:

0 ≤ F (х) ≤1

2. F (х) - неубывающая функция, т.е. F (х)≥ F (х), если х ≥ х.

3.Если возможные значения случайной величины принадлежат интервалу (а, в), то: 1) F (х) = 0 при х ≤ а; 2) F (х) = 1 при х ≥ в.

Плотность распределения

Непрерывную случайную величину можно также задать, используя функцию, называемую плотностью распределения или плотностью вероятности. При этом плотностью распределения вероятности непрерывной случайной величины Х называют функцию f(х) – первую производную от функции распределения F(х): f (х) = F′(х)

Свойства плотности распределения

1. Плотность распределения – неотрицательная функция: f (х) ≥ 0. Геометрически это свойство означает, что точки, принадлежащие графику плотности распределения, расположены либо над осью Ох, либо на этой оси. График плотности распределения называют кривой распределения.

2. Интеграл распределения от плотности распределения в пределах от -∞ до ∞ равен единице: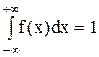

Вероятностный смысл плотности распределения: вероятность того, что случайная величина примет значение, принадлежащее интервалу (х, х + ∆х), приближенно равна произведению плотности вероятности в точке х на длину интервала ∆х.

Геометрически этот результат истолковывается так: вероятность того, что случайная величина примет значение, принадлежащее интервалу (х, ∆х), приближенно равна площади прямоугольника с основанием ∆х и высотой f(х).