1. Общие свойства гармонических функций. Теорема о среднем. Теорема о максимуме и минимуме гармонической функции. Теорема о единственности решения задачи Дирихле.
2. Формула Бернулли (с доказательством).
3. Найти решение задачи Коши для волнового уравнения
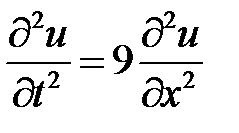 ,
,
НУ: 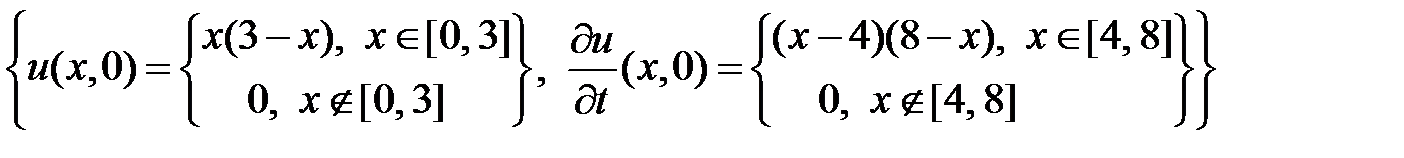 .
.
4. Производится два выстрела с вероятностями попадания в цель, равными 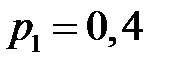 ,
, 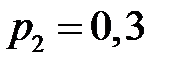 . Найти математическое ожидание общего числа попаданий.
. Найти математическое ожидание общего числа попаданий.
1. Функция 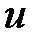 называется гармонической в области
называется гармонической в области 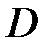 , если она в этой области удовлетворяет уравнению Лапласа, т.е.
, если она в этой области удовлетворяет уравнению Лапласа, т.е.
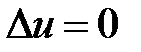 для всех точек области
для всех точек области 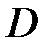 .
.
Рассмотрим основные свойства гармонических функций. Их вывод основан на формуле Грина
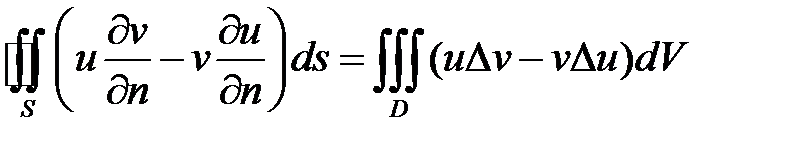 .
.
Свойства гармонических функций:
1. Если 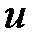 – гармоническая в области
– гармоническая в области 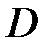 функция,
функция, 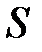 – граница области
– граница области 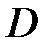 , то
, то 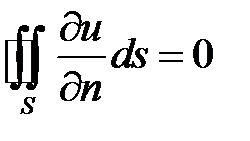 .
.
Доказательство. Во второй формуле Грина возьмем 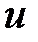 – гармоническая в
– гармоническая в 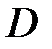 функция (т.е.
функция (т.е. 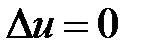 ), а
), а 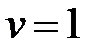 (тогда
(тогда 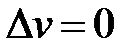 ,
, 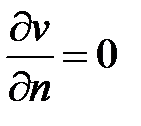 ) и получим
) и получим 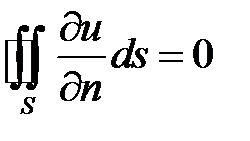 .
.
2. Формула среднего значения (теорема о среднем). Если 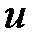 – гармоническая в области
– гармоническая в области 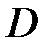 функция, то
функция, то
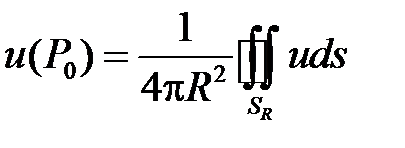 ,
,
где 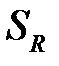 – сфера радиуса
– сфера радиуса 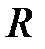 с центром в точке
с центром в точке 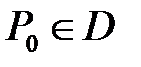 .
.
3. Принцип максимального значения. Если функция 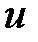 непрерывна в замкнутой области
непрерывна в замкнутой области 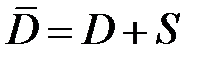 и гармоническая внутри
и гармоническая внутри 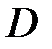 , то она достигает своего наибольшего (наименьшего) значения на поверхности
, то она достигает своего наибольшего (наименьшего) значения на поверхности 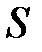 .
.
Отсюда вытекают еще три свойства гармонической функции.
4. Если гармоническая в области 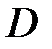 функция и удовлетворяет на границе области условию
функция и удовлетворяет на границе области условию 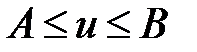 , то она удовлетворяет этому условию и внутри области
, то она удовлетворяет этому условию и внутри области 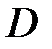 .
.
5. Если гармоническая в области 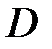 функция и принимает на границе области постоянное значение, то она постоянна и во всей области
функция и принимает на границе области постоянное значение, то она постоянна и во всей области 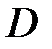 . В частности, если
. В частности, если 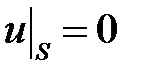 , то
, то 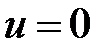 в
в 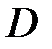 .
.
6. Если функции 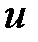 и
и 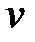 гармоничны в области
гармоничны в области 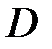 , то выполнимость на границе области неравенства
, то выполнимость на границе области неравенства 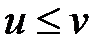 влечет за собой выполнимость этого неравенства и внутри области
влечет за собой выполнимость этого неравенства и внутри области 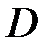 .
.
Теорема о единственности решения задачи Дирихле. Решение внутренней задачи Дирихле
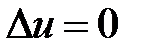 в
в 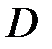 ,
,
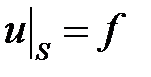 ,
,
непрерывное в замкнутой области 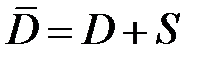 , единственно.
, единственно.
Доказательство. Пусть две функции 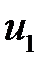 и
и 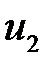 являются решением этой задачи. Тогда их разность
являются решением этой задачи. Тогда их разность 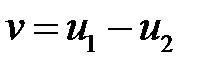 удовлетворяет уравнению Лапласа в области
удовлетворяет уравнению Лапласа в области 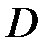 , а на границе
, а на границе 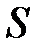 принимает значение, равное нулю. В силу свойства 5 гармонической функции имеем, что
принимает значение, равное нулю. В силу свойства 5 гармонической функции имеем, что 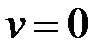 всюду в
всюду в 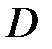 .
.
2. Схемой Бернулли (или последовательностью независимых испытаний) называют последовательность испытаний, удовлетворяющую условиям:
1) в каждом испытании возможны лишь два исхода – появление некоторого события 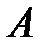 (которое мы будем называть "успехом") или его не появление, т.е. осуществление события
(которое мы будем называть "успехом") или его не появление, т.е. осуществление события 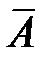 (в этом случае мы будем говорить, что испытание закончилось "неудачей");
(в этом случае мы будем говорить, что испытание закончилось "неудачей");
2) испытания являются независимыми, т.е. исход 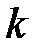 -го испытания не зависит от исходов всех предыдущих испытаний;
-го испытания не зависит от исходов всех предыдущих испытаний;
3) вероятность успеха во всех испытаниях постоянна и равна 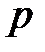 .
.
Вероятность неудачи в каждом испытании обозначим через 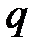 :
: 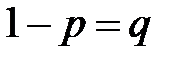 .
.
При рассмотрении схемы Бернулли основной задачей является нахождение вероятности события, состоящего в том, что в 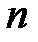 испытаниях успех появится ровно
испытаниях успех появится ровно 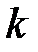 раз,
раз, 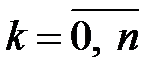 . Обозначим эту вероятность через
. Обозначим эту вероятность через 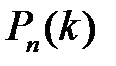 .
.
Теорема. Вероятность 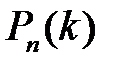 того, что в
того, что в 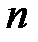 испытаниях по схеме Бернулли произойдет ровно
испытаниях по схеме Бернулли произойдет ровно 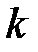 успехов, определяется формулой Бернулли
успехов, определяется формулой Бернулли
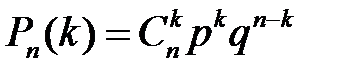 ,
, 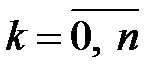 .
.
Доказательство. Обозначим событие "появление успеха" через У, а событие "появление неудачи" через Н. Тогда элементарными исходами последовательности из 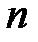 независимых испытаний будут всевозможные цепочки длины
независимых испытаний будут всевозможные цепочки длины 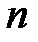 , состоящие из событий У и Н. Всего существует
, состоящие из событий У и Н. Всего существует 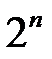 различных цепочек такого вида. Посчитаем вероятности элементарных исходов. В силу независимости испытаний события У, Н, Н,..., У, У являются независимыми и согласно теореме умножения вероятность того, что в
различных цепочек такого вида. Посчитаем вероятности элементарных исходов. В силу независимости испытаний события У, Н, Н,..., У, У являются независимыми и согласно теореме умножения вероятность того, что в 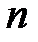 испытаниях успех появился
испытаниях успех появился 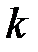 раз, равна
раз, равна 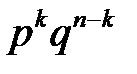 ,
, 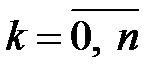 . Поскольку всего существует
. Поскольку всего существует 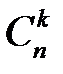 способов расположить
способов расположить 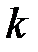 «успехов» среди
«успехов» среди 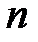 испытаний, то
испытаний, то 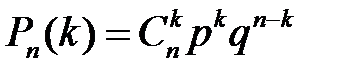 .
.
3. Решение задачи Коши для одномерного волнового уравнения на всей прямой
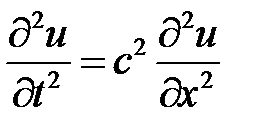 ,
, 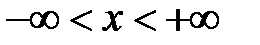 ,
, 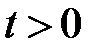 ,
,
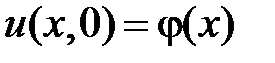 ,
, 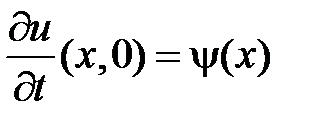 .
.
представляется формулой Даламбера
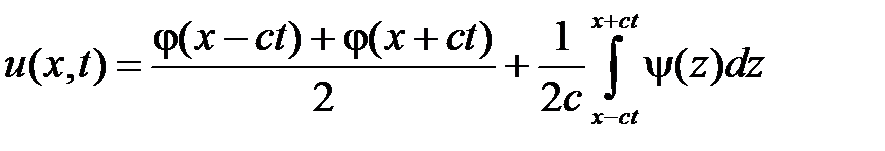 .
.
У нас 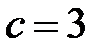 ,
, 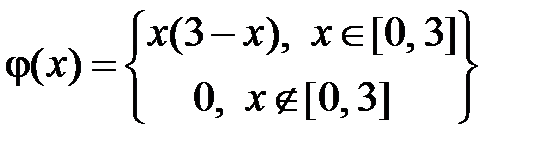 ,
, 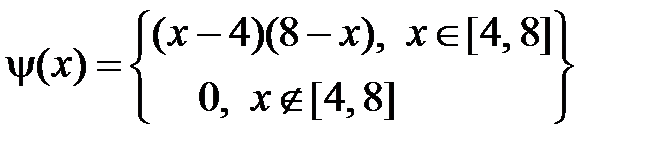 . Тогда
. Тогда
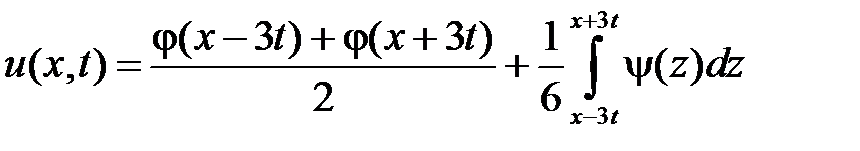 .
.
Для построения решения нарисуем на фазовой плоскости 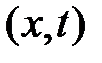 линии характеристик
линии характеристик  ,
, 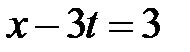 ,
, 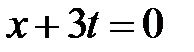 ,
, 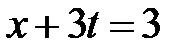 ,
, 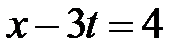 ,
, 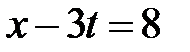 ,
, 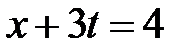 ,
, 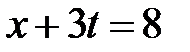 . Эти линии разбивают фазовую плоскость на 15 областей, в каждой из которых нужно найти решение.
. Эти линии разбивают фазовую плоскость на 15 областей, в каждой из которых нужно найти решение.
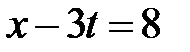
|
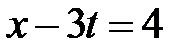
|
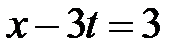
|
|
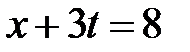
|
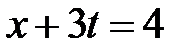
|
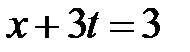
|
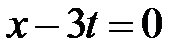
|
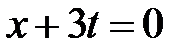
|
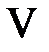
|
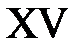
|
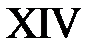
|
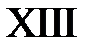
|
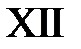
|
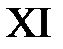
|
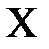
|
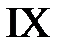
|
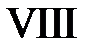
|
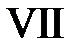
|
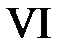
|
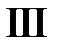
|
|
|
Область I: 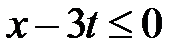 ,
, 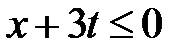 . Тогда в I
. Тогда в I 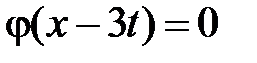 ,
, 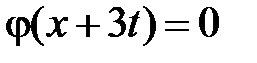 и
и 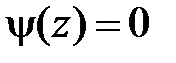 при
при 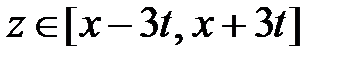 . Значит,
. Значит,
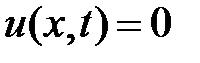 .
.
Область II: 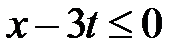 ,
, 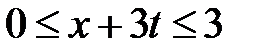 . Тогда в II
. Тогда в II 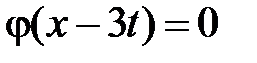 ,
, 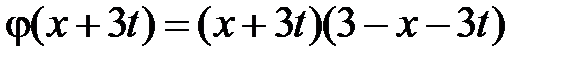 и
и 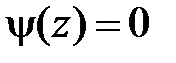 при
при 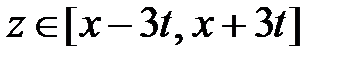 . Значит,
. Значит,
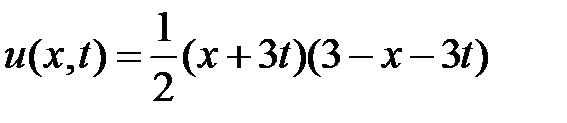 .
.
Область III: 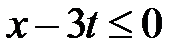 ,
, 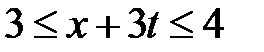 . Тогда в III
. Тогда в III 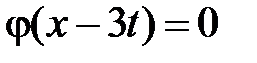 ,
, 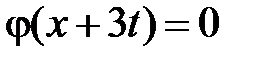 и
и 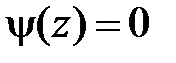 при
при 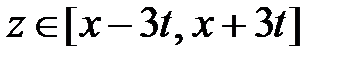 . Значит,
. Значит,
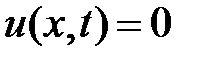 .
.
Область IV: 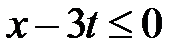 ,
, 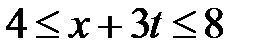 . Тогда в IV
. Тогда в IV 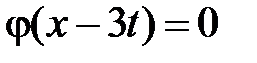 ,
, 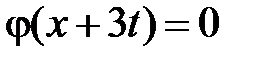 и
и 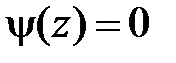 при
при 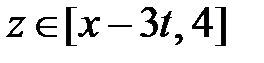 ,
, 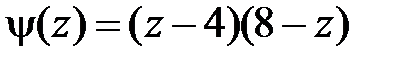 при
при 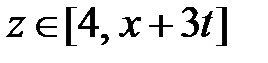 . Значит,
. Значит,
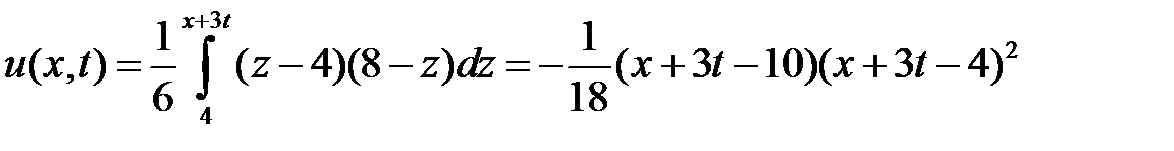 .
.
Область V: 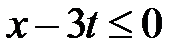 ,
, 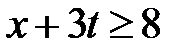 . Тогда в V
. Тогда в V 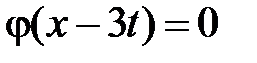 ,
, 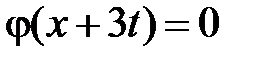 и
и 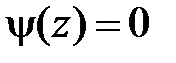 при
при 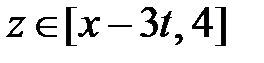 и
и 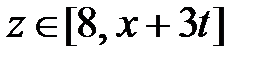 ,
, 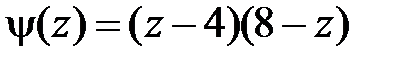 при
при 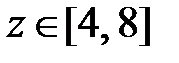 . Значит,
. Значит,
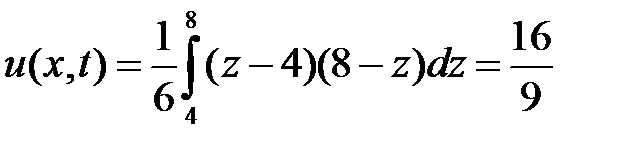 .
.
Область VI: 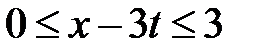 ,
, 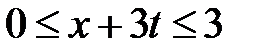 . Тогда в VI
. Тогда в VI 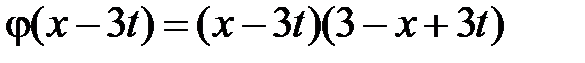 ,
, 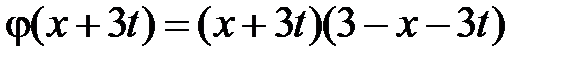 и
и 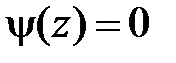 при
при 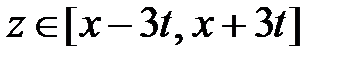 . Значит,
. Значит,
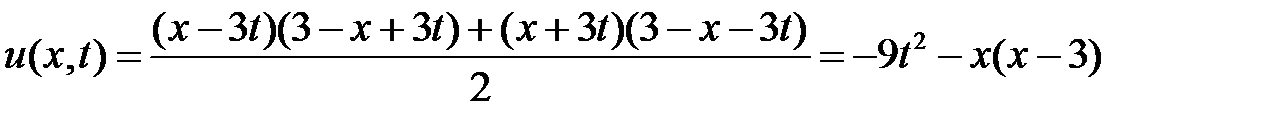 .
.
Область VII: 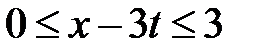 ,
, 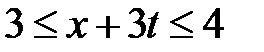 . Тогда в VII
. Тогда в VII 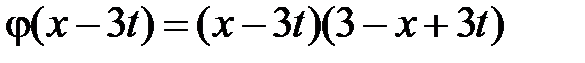 ,
, 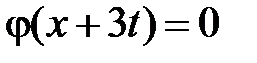 и
и 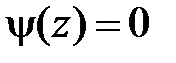 при
при 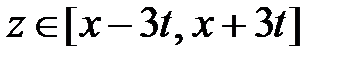 . Значит,
. Значит,
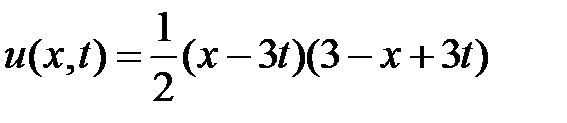 .
.
Область VIII: 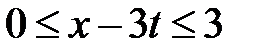 ,
, 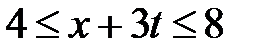 . Тогда в VIII
. Тогда в VIII 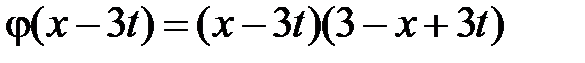 ,
, 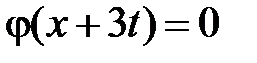 и
и 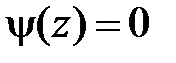 при
при 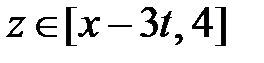 ,
, 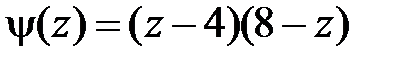 при
при 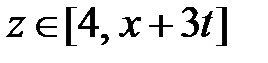 . Значит,
. Значит,
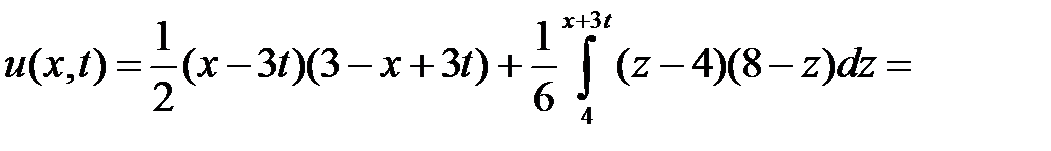
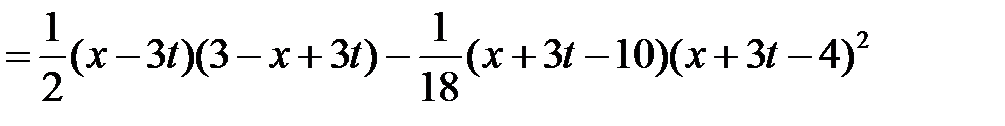 .
.
Область IX: 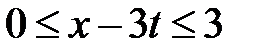 ,
, 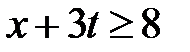 . Тогда в IX
. Тогда в IX 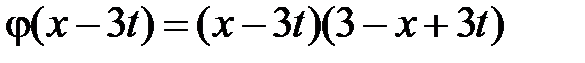 ,
, 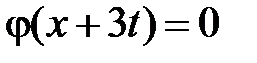 и
и 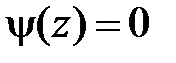 при
при 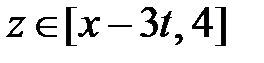 и
и 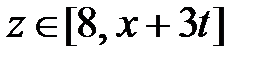 ,
, 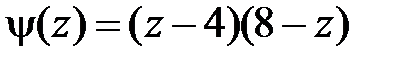 при
при 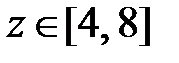 . Значит,
. Значит,
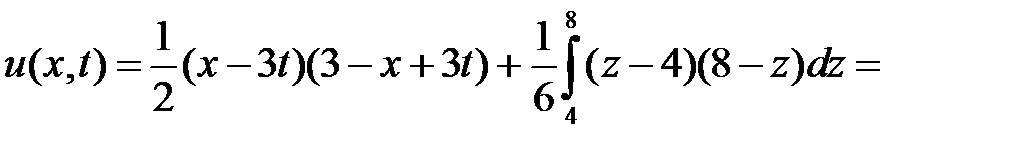
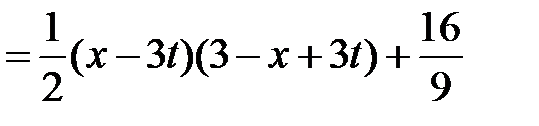 .
.
Область X: 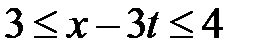 ,
, 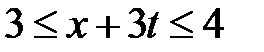 . Тогда в X
. Тогда в X 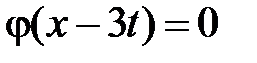 ,
, 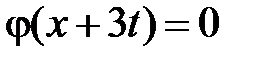 и
и 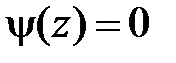 при
при 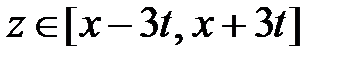 . Значит,
. Значит,
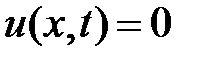 .
.
Область XI: 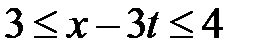 ,
, 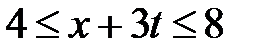 . Тогда в XI
. Тогда в XI 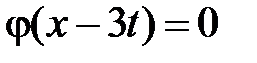 ,
, 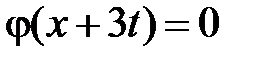 и
и 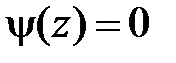 при
при 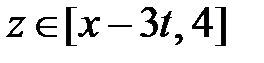 ,
, 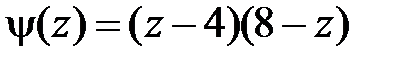 при
при 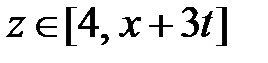 . Значит,
. Значит,
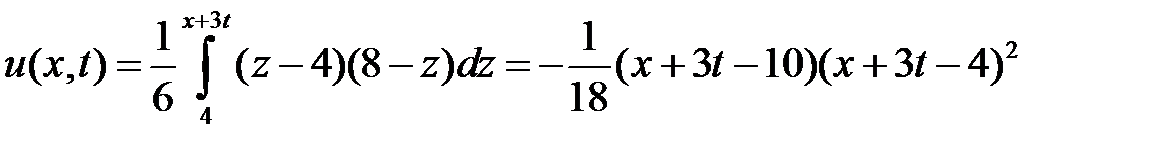 .
.
Область XII: 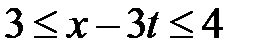 ,
, 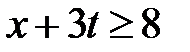 . Тогда в XII
. Тогда в XII 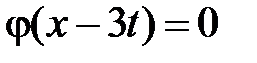 ,
, 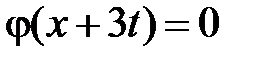 и
и 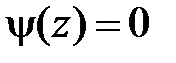 при
при 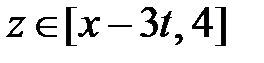 и
и 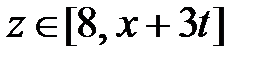 ,
, 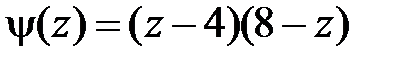 при
при 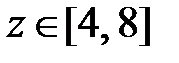 . Значит,
. Значит,
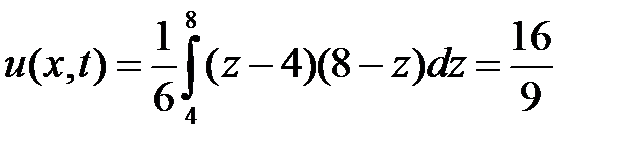 .
.
Область XIII: 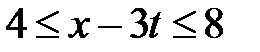 ,
, 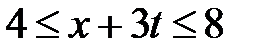 . Тогда в XIII
. Тогда в XIII 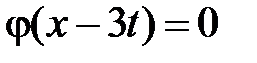 ,
, 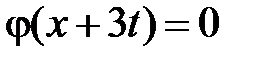 и
и 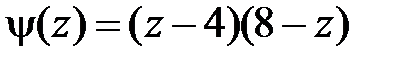 при
при 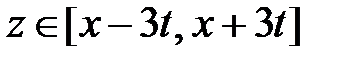 . Значит,
. Значит,
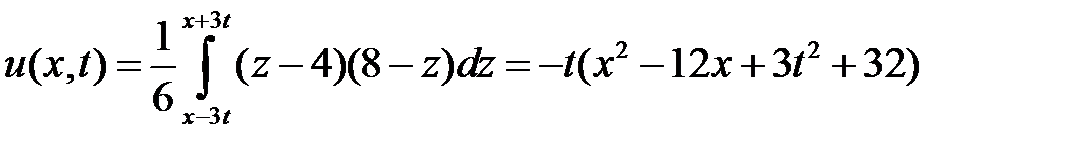 .
.
Область XIV: 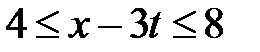 ,
, 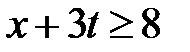 . Тогда в XIV
. Тогда в XIV 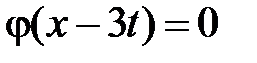 ,
, 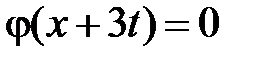 и
и 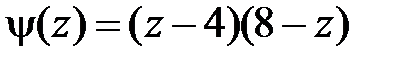 при
при 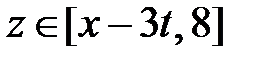 ,
, 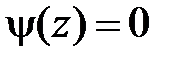 при
при 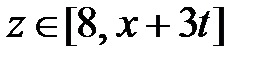 . Значит,
. Значит,
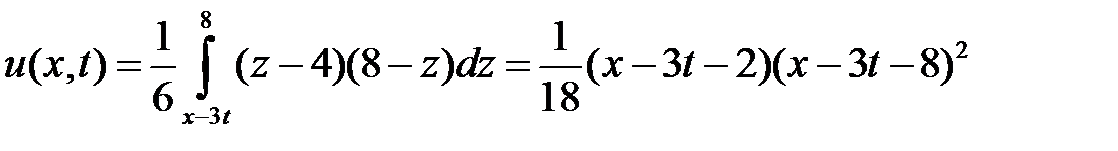 .
.
Область XV: 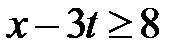 ,
, 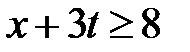 . Тогда в XV
. Тогда в XV 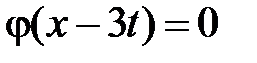 ,
, 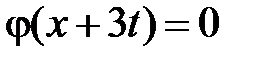 и
и 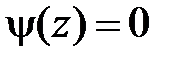 при
при 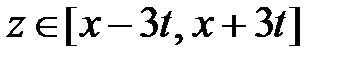 . Значит,
. Значит,
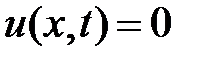 .
.
4. Сначала составим ряд распределения случайной величины 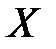 – общее число попаданий в цель при двух выстрелах. Случайная величина
– общее число попаданий в цель при двух выстрелах. Случайная величина 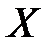 может принимать значения 0, 1, 2. Введем в рассмотрение события
может принимать значения 0, 1, 2. Введем в рассмотрение события
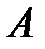 – в цель попали первым выстрелом;
– в цель попали первым выстрелом;
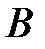 – в цель попали вторым выстрелом.
– в цель попали вторым выстрелом.
Тогда
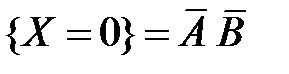 ,
, 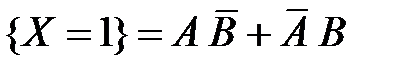 ,
, 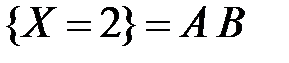 .
.
По условию
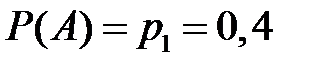 ,
, 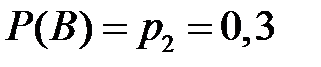 .
.
Значит, вероятности промахов
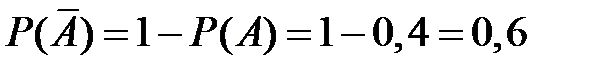 ,
, 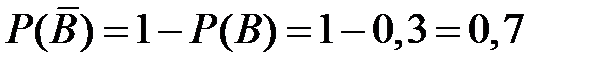 .
.
Находим ряд распределения (считая, что стрелки независимо друг от друга попадают в мишень или промахиваются)
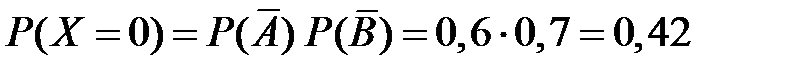 ,
,
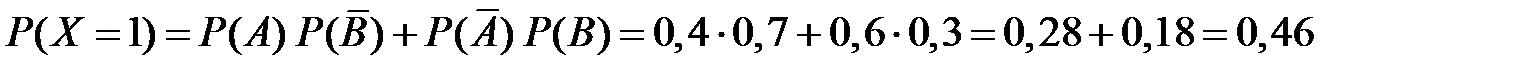 ,
,
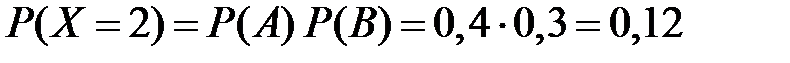 .
.
Проверим условие нормировки:
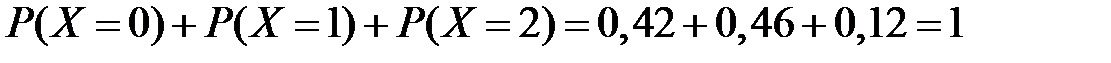 .
.
Ряд распределения приведен в таблице:
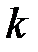
| |||
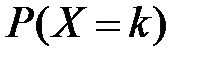
| 0,42 | 0,46 | 0,12 |
Находим математическое ожидание:
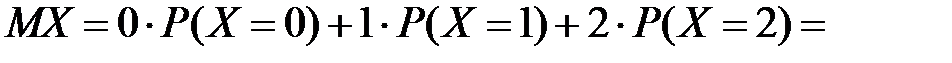
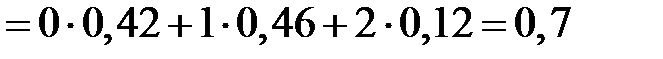 .
.
 2015-07-14
2015-07-14 462
462








