1. Задача Неймана для уравнения Лапласа. Условие разрешимости.
2. Формула полной вероятности (с доказательством). Формула Байеса.
3. Решить смешанную задачу для волнового уравнения
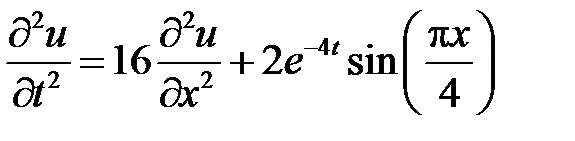 ,
, 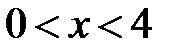 ,
,
ГУ: 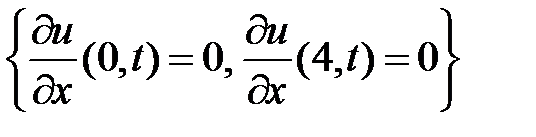 ; НУ:
; НУ: 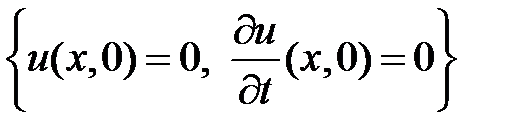 .
.
4. Случайная величина 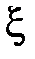 задана плотностью вероятности
задана плотностью вероятности 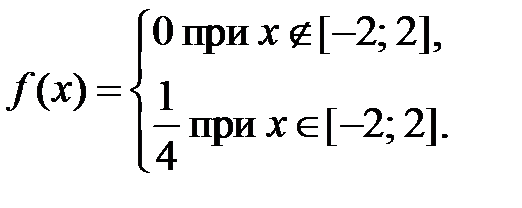 Найти
Найти 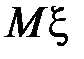 и
и 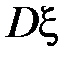 . (в билете опечатка: для приведенной в нем плотности не выполняется условие нормировки, я исправил как надо)
. (в билете опечатка: для приведенной в нем плотности не выполняется условие нормировки, я исправил как надо)
1. Задача Неймана для уравнения Лапласа имеет вид:
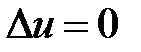 в области
в области  ,
,
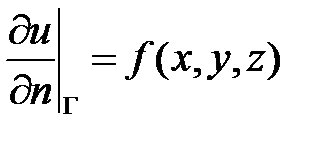 ,
,
где 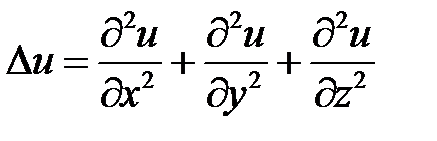 – оператор Лапласа,
– оператор Лапласа, 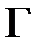 – граница области
– граница области  ,
, 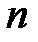 – нормаль к границе.
– нормаль к границе.
Задача Неймана имеет решение не для любой функции 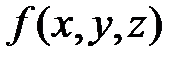 , а только для такой, для которой выполнено условие
, а только для такой, для которой выполнено условие
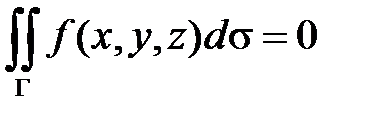
(поверхностный интеграл по границе области равен нулю).
Докажем это условие. Во второй формуле Грина
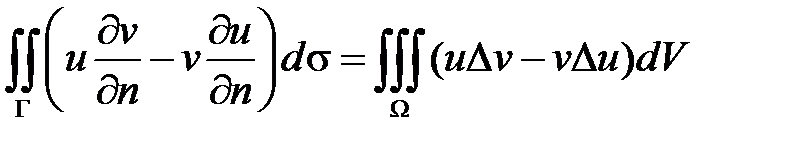
возьмем 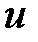 – гармоническая в
– гармоническая в  функция (т.е.
функция (т.е. 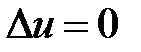 ), а
), а 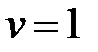 (тогда
(тогда 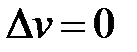 ,
, 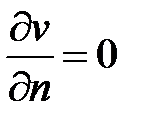 ).
).
Тогда формула Грина примет вид
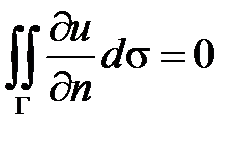 ,
,
откуда с учетом условия Неймана 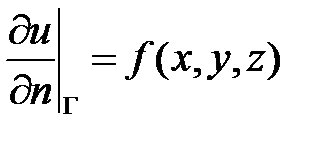 и получаем условие разрешимости в виде
и получаем условие разрешимости в виде
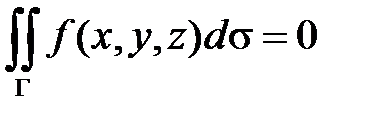
Если условие разрешимости выполнено, то задача Неймана для уравнения Лапласа имеет бесчисленное множество решений.
2. События 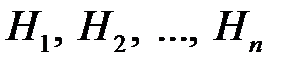 образуют полную группу попарно несовместных событий, если:
образуют полную группу попарно несовместных событий, если:
а) они являются попарно несовместными, т.е. 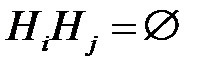 при
при  ;
;
б) 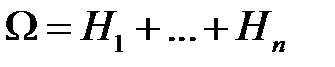 .
.
Теорема. Пусть 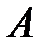 – некоторое событие, а события
– некоторое событие, а события 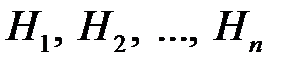 образуют полную группу попарно несовместных событий. Тогда имеет место формула полной вероятности
образуют полную группу попарно несовместных событий. Тогда имеет место формула полной вероятности
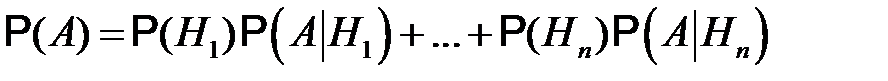 .
.
Доказательство. Заметим, что событие 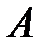 можно представит в виде суммы попарно несовместных событий (рис.):
можно представит в виде суммы попарно несовместных событий (рис.):
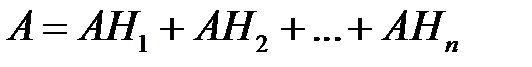 .
.
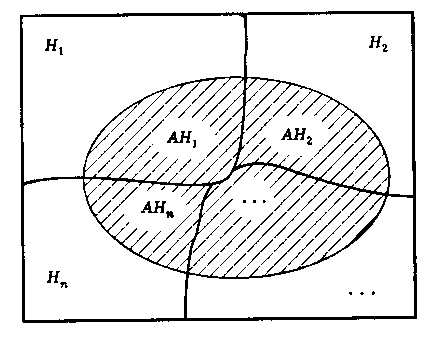
Рис.
Используя теорему сложения, получим
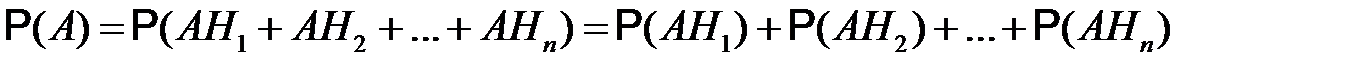 .
.
Применяя к слагаемым последней суммы теорему умножения
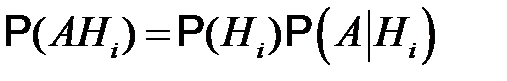 ,
,
получим
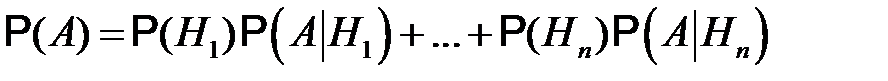 .
.
События 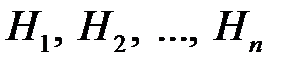 называют гипотезами.
называют гипотезами.
Часто бывает, что событие 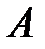 может происходить при двух взаимоисключающих условиях
может происходить при двух взаимоисключающих условиях 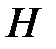 и
и 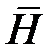 . Если
. Если 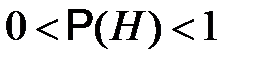 , то события
, то события  и
и 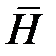 образуют полную группу событий и формулу полной вероятности можно записать в виде
образуют полную группу событий и формулу полной вероятности можно записать в виде
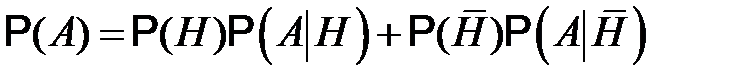 .
.
Теорема. Пусть события 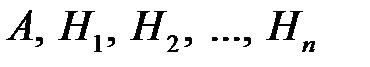 удовлетворяют условиям, сформулированным в условии теоремы о формуле полной вероятности и
удовлетворяют условиям, сформулированным в условии теоремы о формуле полной вероятности и 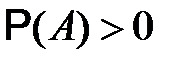 . Тогда справедлива формула Байеса
. Тогда справедлива формула Байеса
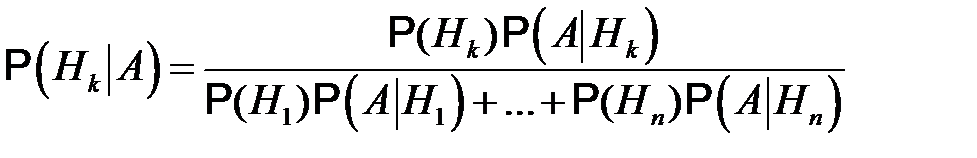 .
.
Доказательство. Используя определение условной вероятности, получим
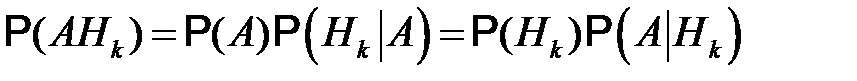 ,
,
откуда
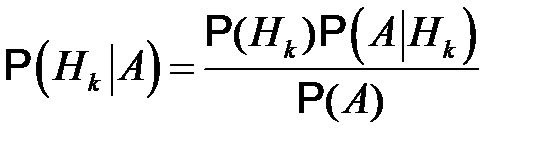 .
.
Далее, расписав в знаменателе 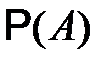 по формуле полной вероятности, получим формулу Байеса.
по формуле полной вероятности, получим формулу Байеса.
Вероятности гипотез 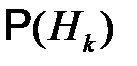 называют еще априорными вероятностями, а вероятности
называют еще априорными вероятностями, а вероятности 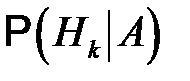 – апостериорными вероятностями (
– апостериорными вероятностями (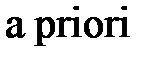 – до опыта,
– до опыта, 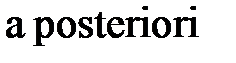 – после опыта).
– после опыта).
Если гипотезы две – 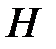 и
и 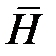 , то формулы Байеса для апостериорных вероятностей имеет вид
, то формулы Байеса для апостериорных вероятностей имеет вид
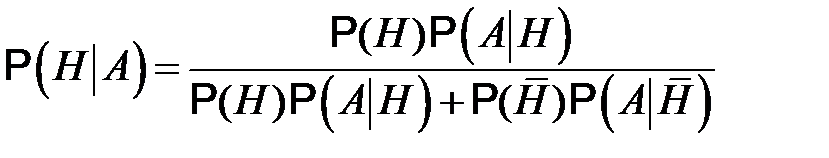 ,
, 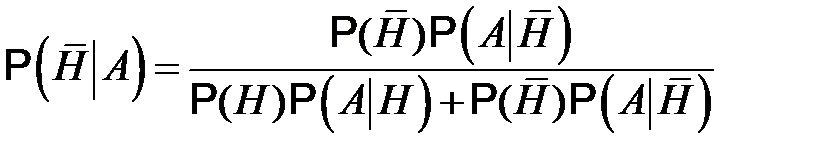 .
.
3. Сначала найдем общее решение однородного уравнения 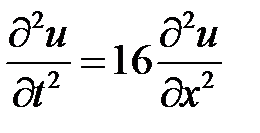 при нулевых граничных условиях. Для этого воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения
при нулевых граничных условиях. Для этого воспользуемся методом Фурье (разделения переменных). Нетривиальные решения уравнения 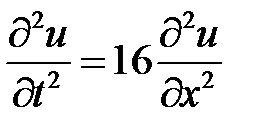 будем искать в виде
будем искать в виде 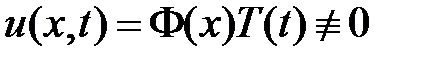 . Подставляем в уравнение и разделяем переменные:
. Подставляем в уравнение и разделяем переменные:
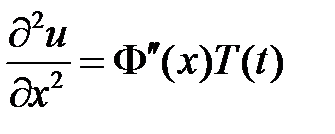 ,
, 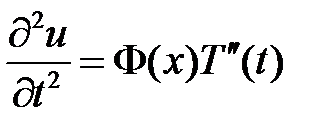 ,
,
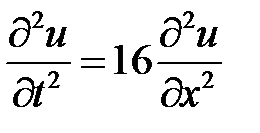 :
: 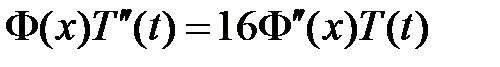 ,
,
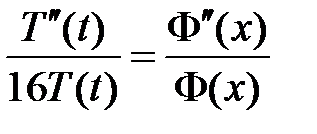 ,
, 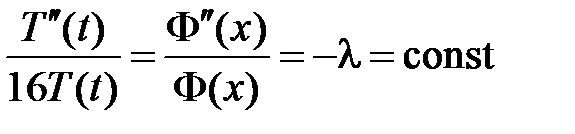 ,
, 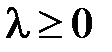 .
.
Тогда функции 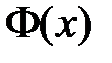 и
и 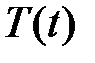 являются соответственно решениями уравнений
являются соответственно решениями уравнений
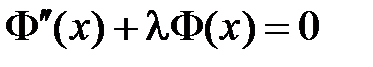 ,
, 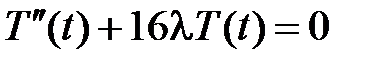 .
.
Из граничных условий 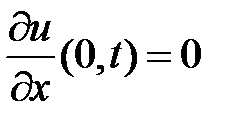 ,
, 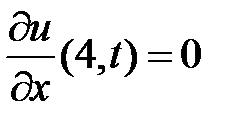 получаем краевые условия для функции
получаем краевые условия для функции 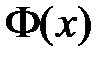 :
: 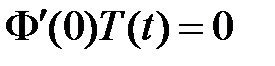 ,
, 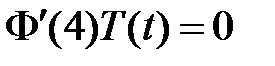 , значит,
, значит, 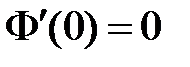 ,
, 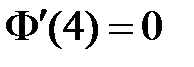 . Таким образом, для определения
. Таким образом, для определения 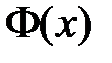 и
и 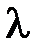 получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля
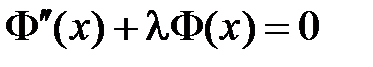
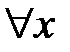 :
: 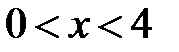 ,
,
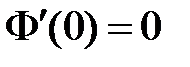 ,
, 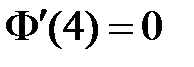 .
.
Поскольку мы имеем дело со второй краевой задачей, то 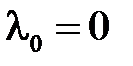 является собственным значением, а
является собственным значением, а 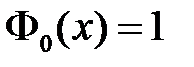 – соответствующей ему собственной функцией.
– соответствующей ему собственной функцией.
Пусть теперь 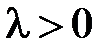 (при
(при 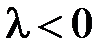 задача имеет только тривиальные решения). Общее решение уравнения
задача имеет только тривиальные решения). Общее решение уравнения 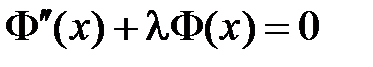 имеет вид
имеет вид
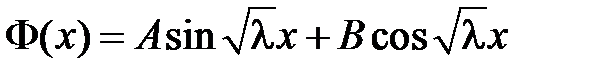 .
.
Тогда 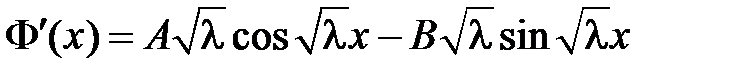 . Из краевого условия
. Из краевого условия 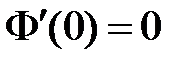 получаем:
получаем: 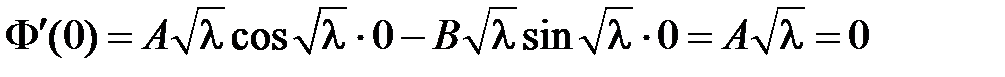 ,
, 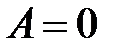 , т.е.
, т.е. 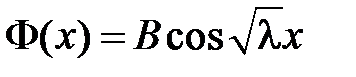 и
и 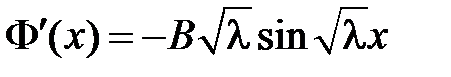 .
.
Из краевого условия 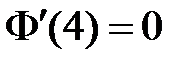 получаем:
получаем: 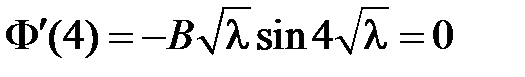 . Поскольку
. Поскольку 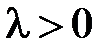 и
и 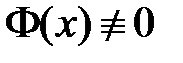 , то
, то 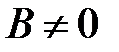 и равенство
и равенство 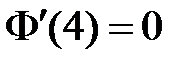 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 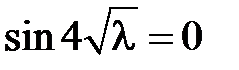 , откуда получаем
, откуда получаем 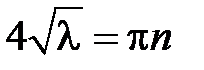 ,
, 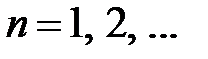 , т.е.
, т.е. 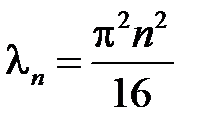 ,
, 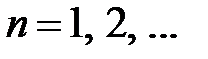 . Тогда получим
. Тогда получим 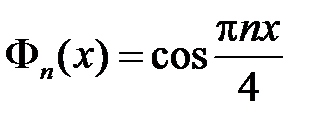 ,
, 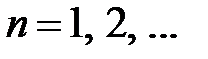 . Таким образом, получили решение задачи Штурма-Лиувилля:
. Таким образом, получили решение задачи Штурма-Лиувилля:
собственные значения 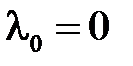 ,
, 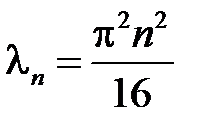 ,
, 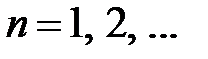 ;
;
собственные функции 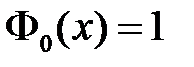 ,
, 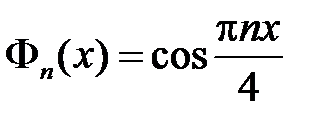 ,
, 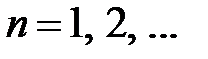 .
.
Разложим функцию 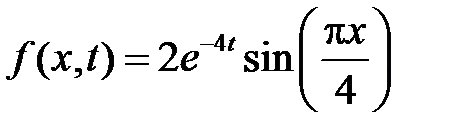 в ряд Фурье на отрезке
в ряд Фурье на отрезке 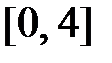 по системе собственных функций
по системе собственных функций 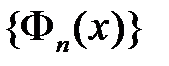 :
:
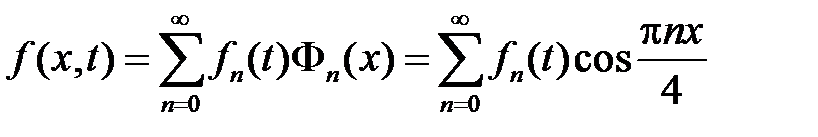 ,
,
где
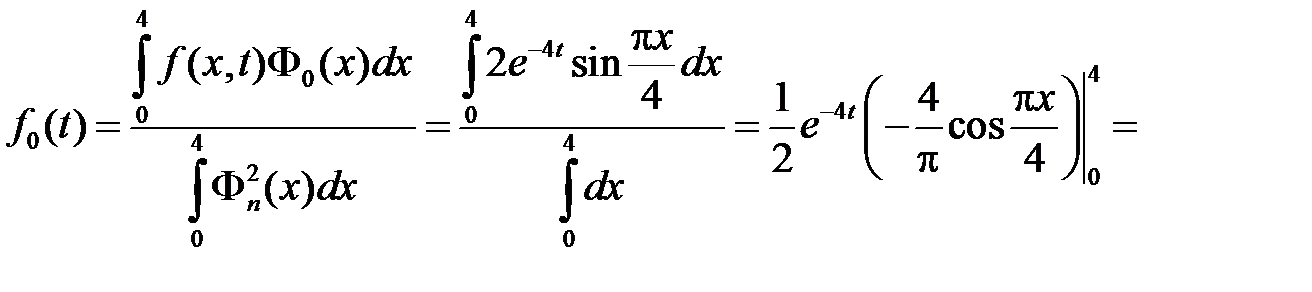
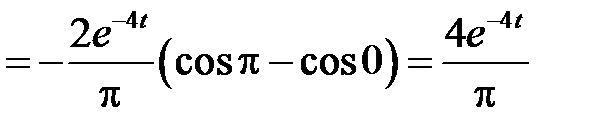 ,
,
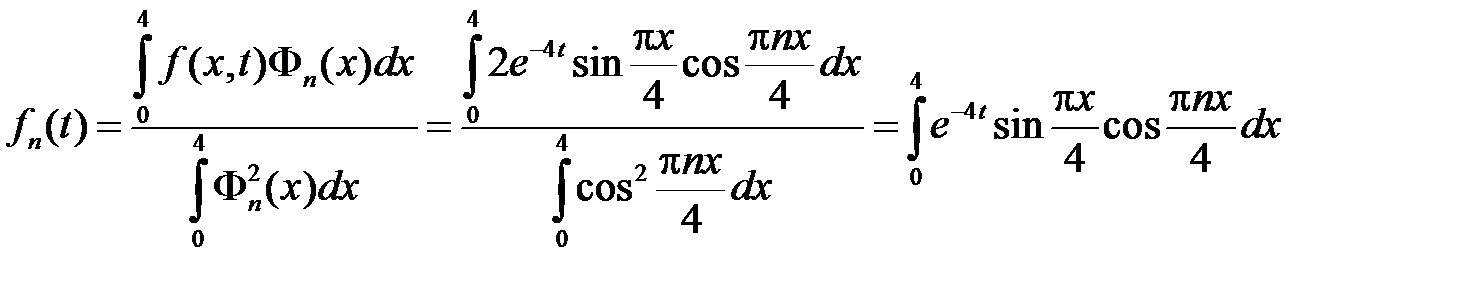 ,
,
так как
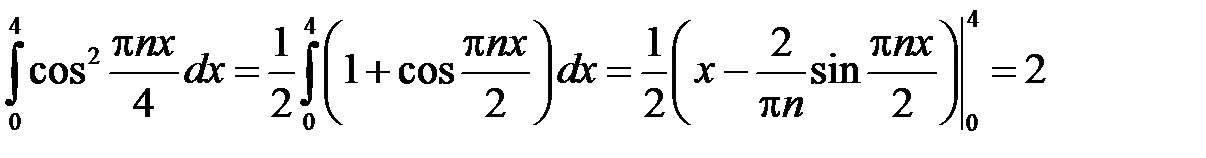 ,
,
Находим:
при 
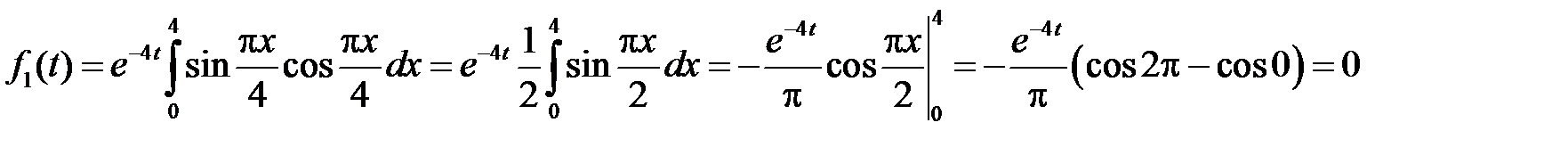 ,
,
при 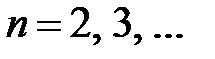
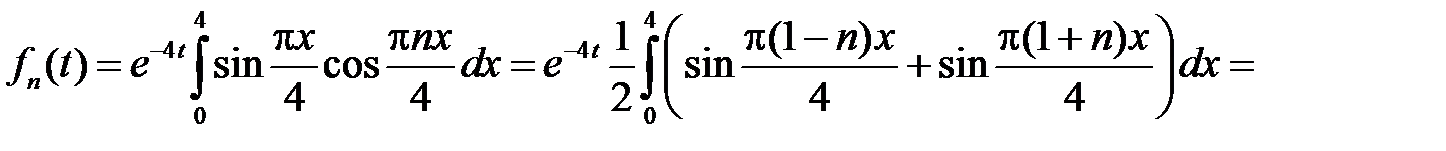
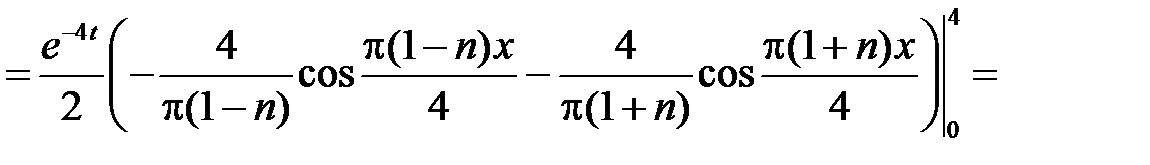
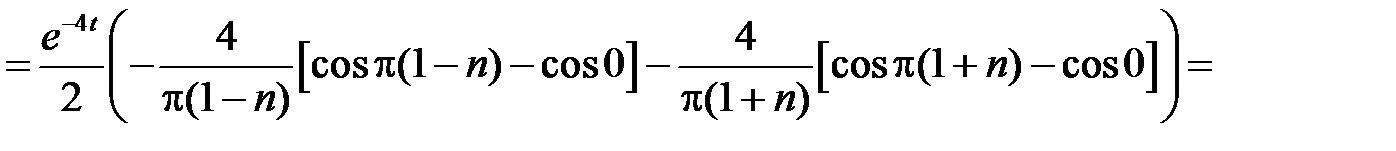
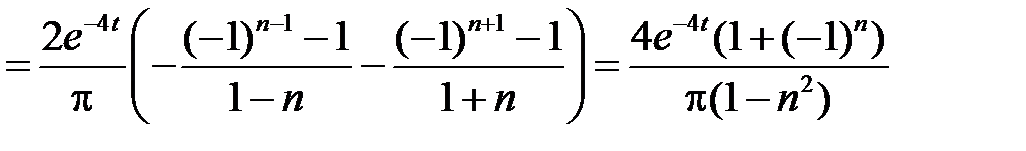 .
.
Заметим, что
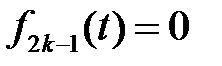 ,
, 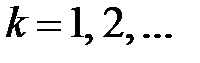 ,
,
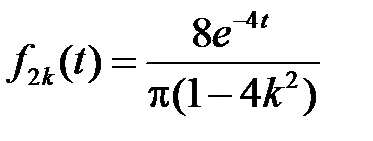 ,
, 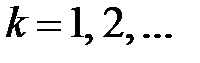 .
.
Тогда
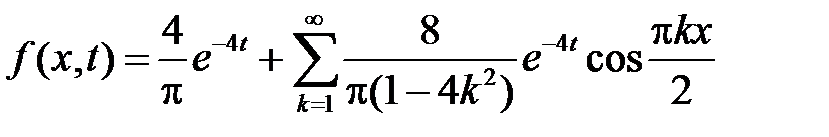 .
.
Решение смешанной задачи для неоднородного волнового уравнения будем искать в виде ряда
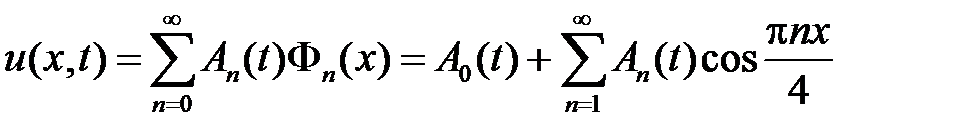 ,
,
где функции 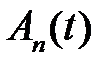 ,
, 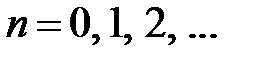 , подберем так, чтобы удовлетворить неоднородному уравнению и начальным условиям. Заметим, что функция
, подберем так, чтобы удовлетворить неоднородному уравнению и начальным условиям. Заметим, что функция 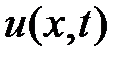 при любом выборе функций
при любом выборе функций 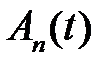 ,
, 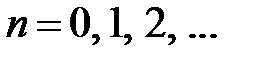 , точно удовлетворяет однородным граничным условиям
, точно удовлетворяет однородным граничным условиям 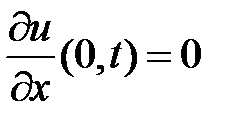 ,
, 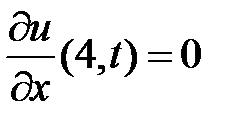 . Находим производные
. Находим производные
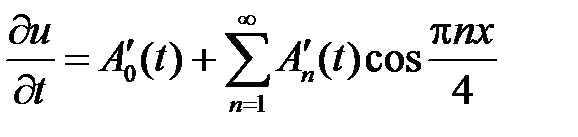 ,
, 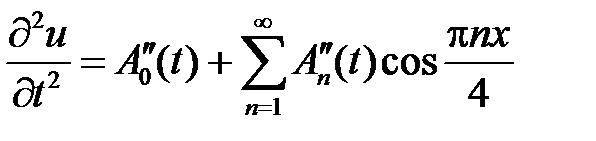 ,
,
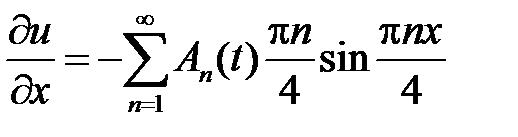 ,
, 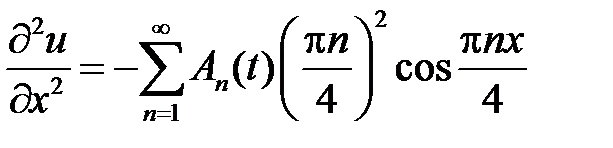
и подставляем их в неоднородное уравнение:
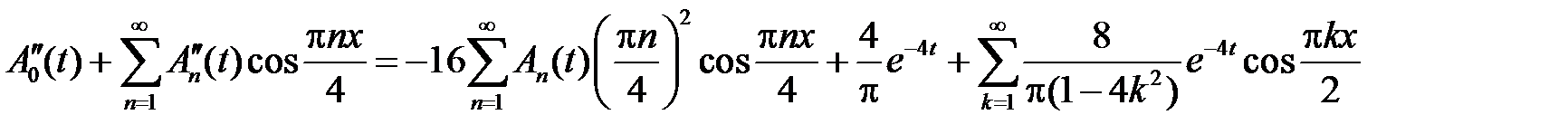 ,
,
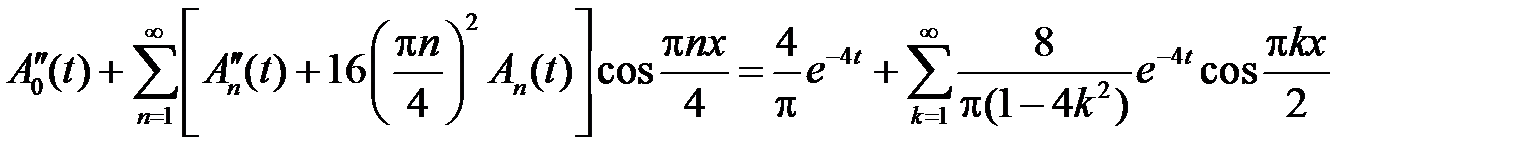 ,
,
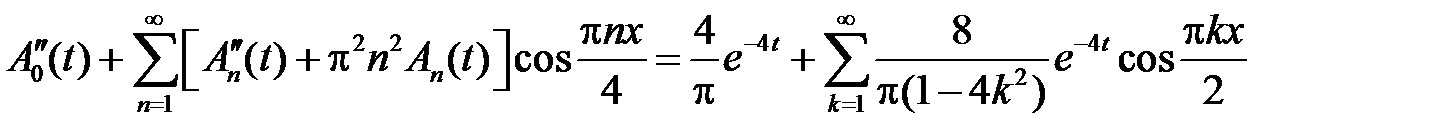 ,
,
откуда получим, что функции 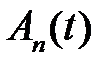 ,
, 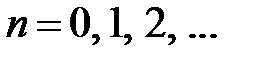 , удовлетворяют уравнениям
, удовлетворяют уравнениям
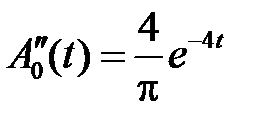 ,
,
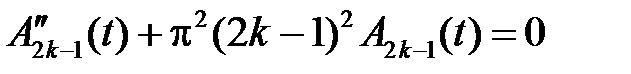 ,
, 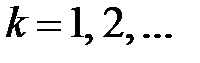 ,
,
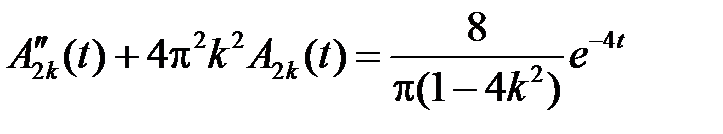 .
.
Из начальных условий получаем:
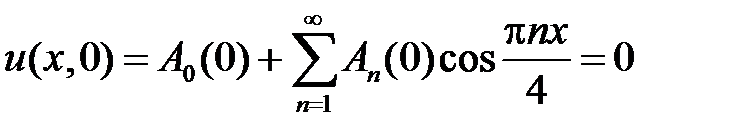 ,
,
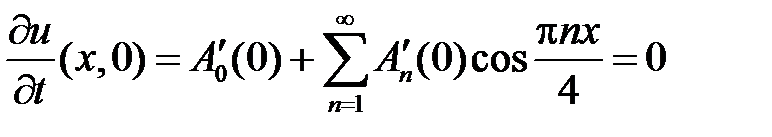 ,
,
откуда
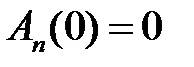 ,
, 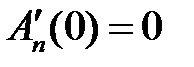 .
.
Итак, функции 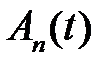 ,
, 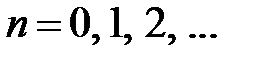 , являются решениями задач Коши
, являются решениями задач Коши
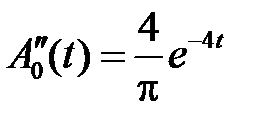 ,
, 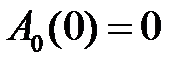 ,
, 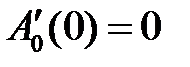 ;
;
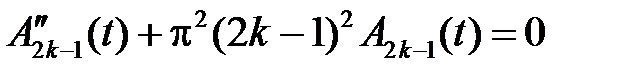 ,
, 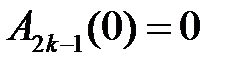 ,
, 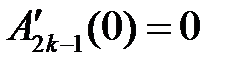
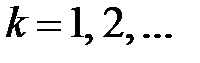 ;
;
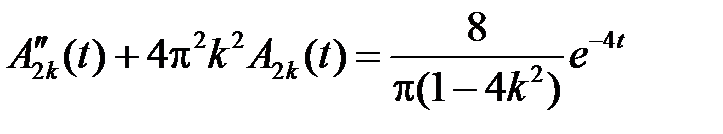 ,
, 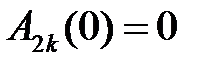 ,
, 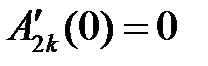
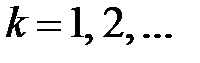 .
.
Решаем задачу для 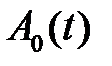 :
:
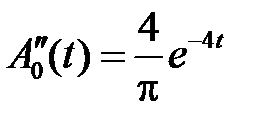
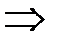
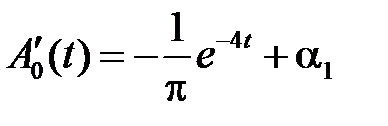 ,
, 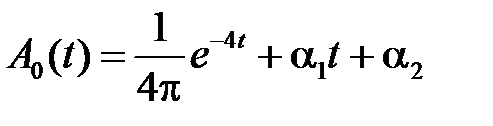 ,
,
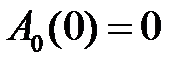 :
: 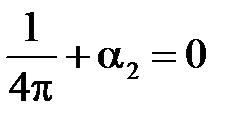 ,
, 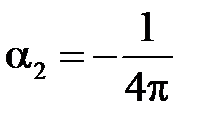 ,
,
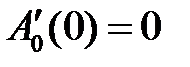 :
: 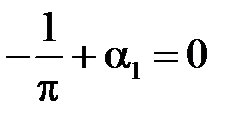 ,
, 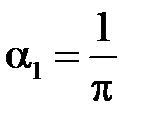 .
.
Тогда
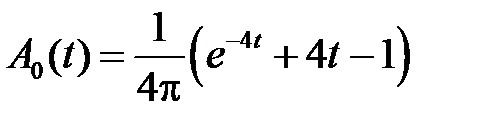
Задачи для 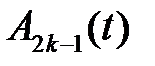 ,
, 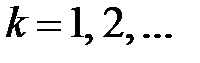 , имею в силу единственности только нулевое решение:
, имею в силу единственности только нулевое решение:
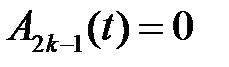 ,
, 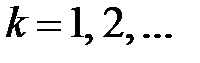 .
.
Решаем задачи для 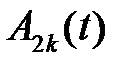 . Уравнение
. Уравнение 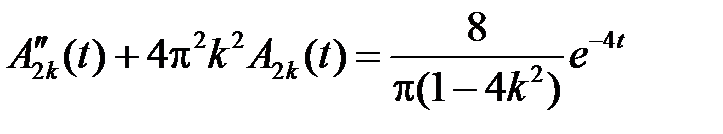 – неоднородное линейное уравнение второго порядка с постоянными коэффициентами. Общее решение соответствующего однородного имеет вид
– неоднородное линейное уравнение второго порядка с постоянными коэффициентами. Общее решение соответствующего однородного имеет вид
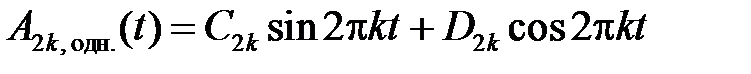 .
.
Частное решение неоднородного уравнения будем искать в виде
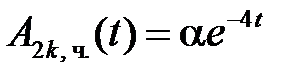 .
.
Тогда
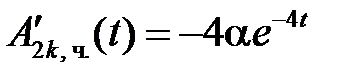 ,
, 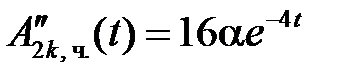 ,
,
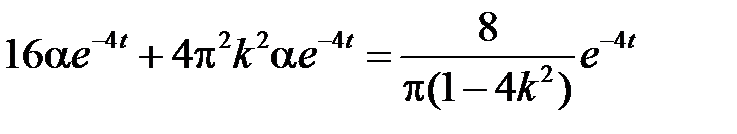 ,
,
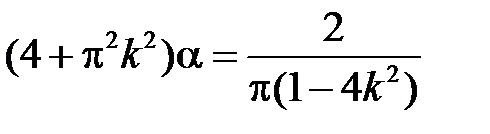 ,
, 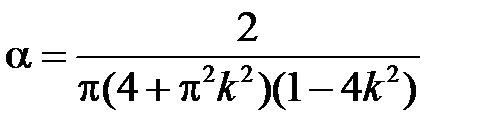
Значит, общее решение уравнения для 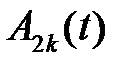 есть
есть
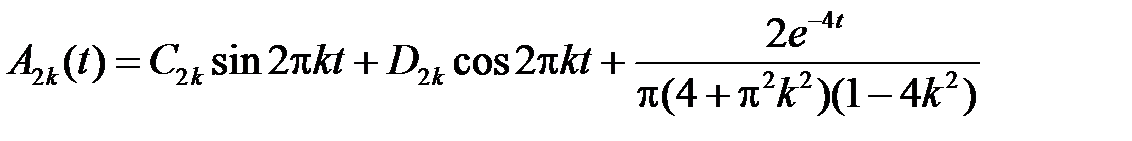 .
.
Найдем 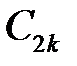 ,
, 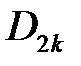 из начальных условий:
из начальных условий:
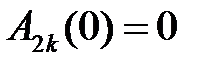 :
: 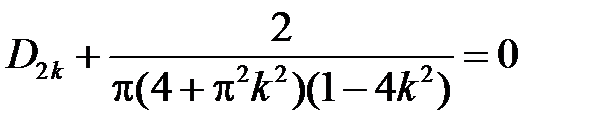 ,
, 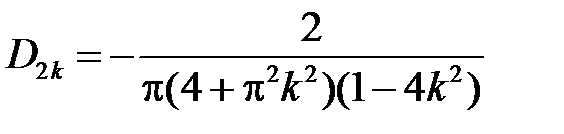 ,
,
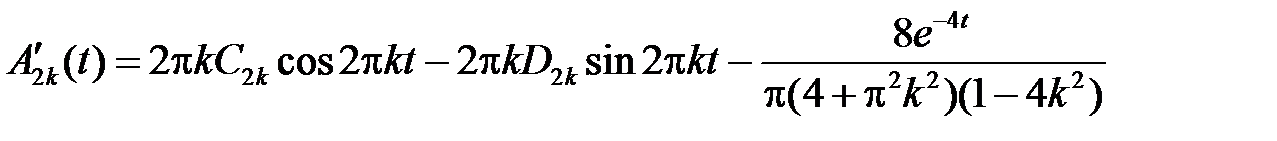 ,
,
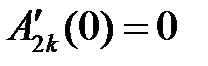 :
: 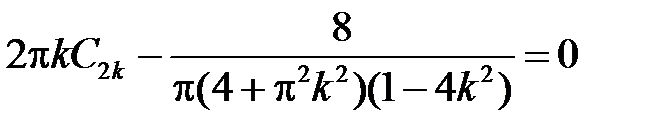 ,
, 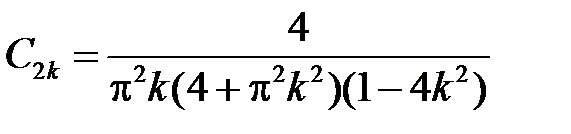
Итак,
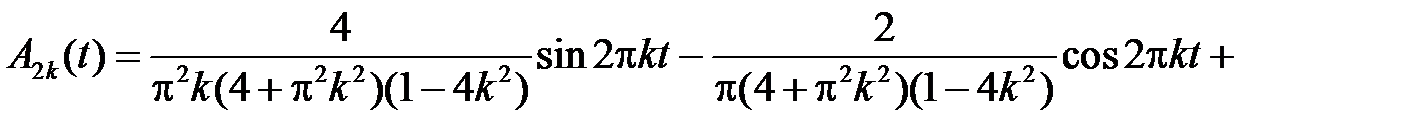
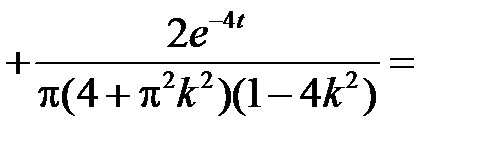
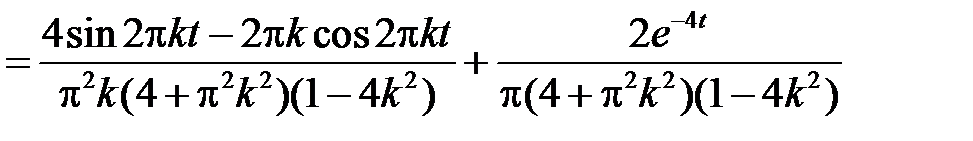 .
.
Окончательно получим решение смешанной задачи для неоднородного волнового уравнения при нулевых граничных условиях в виде
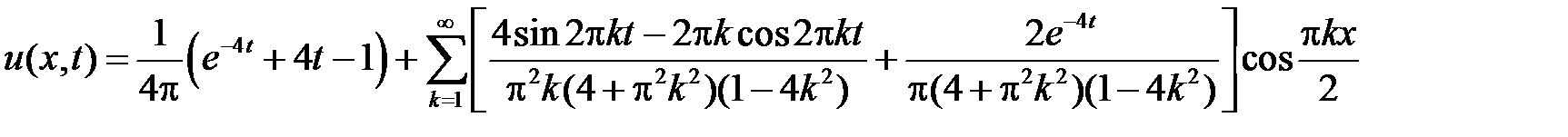 .
.
4. Математическое ожидание и дисперсию найдем соответственно по формулам:
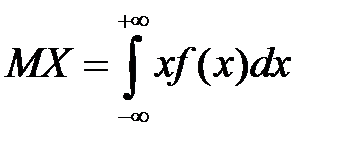 ,
, 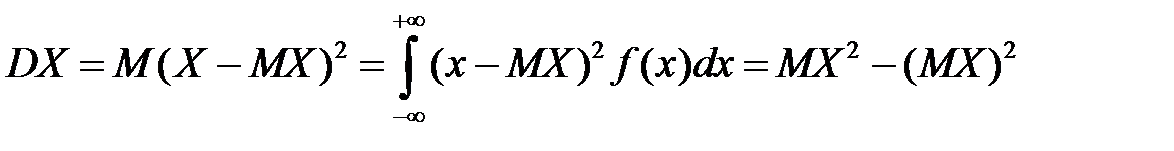 .
.
Для заданной плотности имеем:
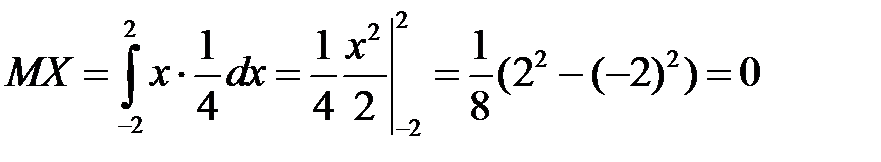 ,
,
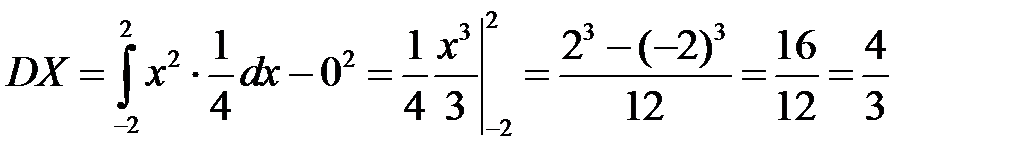 .
.
 2015-07-14
2015-07-14 964
964