Введение

Для восприятия курса как математической головоломки, разбираясь в которой испытываешь ни с чем не сравнимое ощущение компетентности и уверенности в себе, необходимо освежить в памяти некоторые математические понятия и конструкции. Признаком, говорящим о том, что вы справились с этой задачей, является наслаждение от прочтения этого введения.

Отношение эквивалентности

Говорят, что на непустом множестве 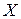задано отношение 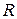, если выбрано подмножество (обозначим его тем же символом) 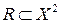. При этом, если 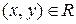, то говорят, что элемент 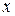находится в отношении 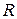с элементом 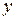и пишут .

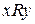Если

o 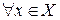имеем 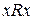, то отношение 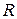называется рефлексивным,

o 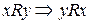, то отношение 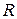называется симметричным,

o 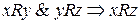, то отношение 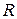называется транзитивным.

Отношение 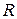называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Если на 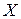задано отношение эквивалентности 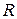, то любые два элемента этого множества либо эквивалентны, либо не эквивалентны. Подмножества множества 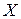, состоящие из всех эквивалентных между собой элементов, называются классами эквивалентности. Различные классы эквивалентности определяют разбиение множества 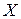: они не пусты, не пересекаются, и их объединение совпадает с 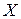. Это, в частности, можно трактовать так: выбрав отношение эквивалентности, мы определяем соответствующую классификацию элементов в .

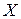Верно и обратное: если на 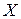задано разбиение, то естественным образом строится отношение эквивалентности

,

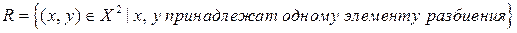для которого классы эквивалентности будут совпадать с элементами разбиения.

Примерами отношений эквивалентности могут быть отношения подобия и равенства треугольников на евклидовой плоскости. В первом случае эквивалентные треугольники называют подобными, во втором – равными.

Точечные евклидовы пространства

Пусть 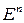– 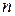-мерное точечное евклидово пространство над вещественным векторным пространством 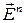(здесь и далее верхний индекс 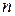– это дополнительная информация о том, что на множестве 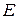определена структура 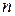-мерного точечного евклидова пространства). Это, в частности, означает, что

1) задано отображение (назовем его отображением Вейля)

,

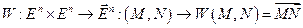обладающее свойствами

а)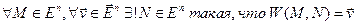

б)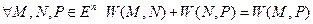

2) на 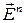задано скалярное произведение – билинейная симметрическая положительноопределенная форма

.

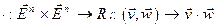По сути, определяет отображение

,

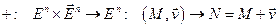которое называют откладыванием вектора от точки, при этом про точку 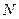говорят, что она получается при откладывании вектора 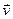от точки .

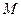Точк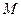и и 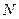в называют соответственно началом и концом вектора 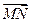, что указывает лишь на историю возникновения вектора .

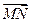Формула

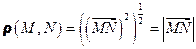
определяет в 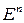расстояние ρ между точками. Аффинные преобразования, сохраняющие расстояние между точками, называются движениями пространства .

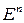Базис и репер как отображения.

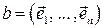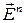Ортонормированный базис в определяет отображение (обозначим его тем же символом)

,

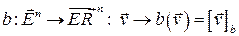где 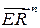– множество 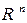, состоящее из 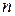-столбцов, со стандартной структурой евклидова векторного пространства и 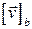‑ координатный столбец вектора 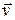в базисе 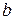, то есть .

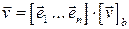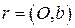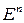Аналогично, для ортонормированного репера в определяется отображение

,

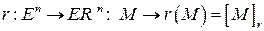где 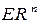– множество 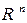со стандартной структурой точечного евклидова пространства над векторным пространством 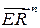, определяемой отображением Вейля

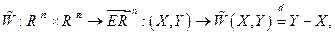
и 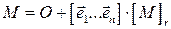, то есть 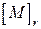‑ координатный столбец точки 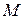в репере 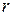. При этом

.

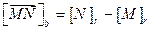Если понятно из контекста, в каком базисе (репере) рассматриваются координаты, вместо 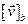(соответственно 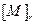) пишут 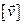(соответственно ).

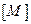Используя введенные выше обозначения, равенство можно переписать так:

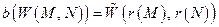
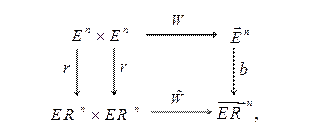
или изобразить в виде коммутативной диаграммы

Разглядывая, постарайтесь найти повод удивиться и задуматься над следующим

· наблюдением:

Какое бы отображение Вейля W ни задать, отображения и переведут его в одно и то же отображение Вейля 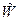, Это говорит, во-первых, о том, что эти отображения обладают неким специфическим свойством, которое принято называть сохранением структуры, а во-вторых, о том, что изучение геометрии пространства 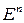сводится к изучению геометрии координатного пространства 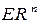(примером, как это делается служит координатное выражение отображений – см. далее).

· вопросом:

Допустим, что b – отображение типа. Какой должна быть биекция r, чтобы отображение 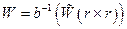было отображением Вейля, то есть определяло на E структуру точечного евклидова пространства?

Координатное выражение отображений.

Пусть в 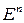выбран репер 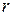, а значит, задано биективное (обратимое) отображение. Тогда для отображений вида 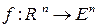и 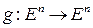их координатные выражения 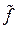и 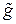однозначно определяются требованием коммутативности диаграмм

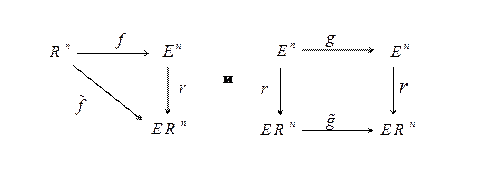
соответственно.

Аналогично определяется понятие координатного выражения отображений векторных пространств.

В принципе, в этом заключен великий смысл координатного метода: он при помощи отображений и дает возможность сводить изучение объектов пространства, где определены координаты, к изучению объектов в (координатном) пространстве n -столбцов. Это возможно, благодаря удивительному свойству отображений и сохранять структуру пространств.

Скалярное произведение в координатах (еще один пример координатного выражения отображений).

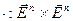
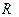
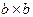
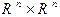
Выбор базиса в 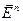однозначно определяет отображение 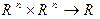, изображенное на коммутативной диаграмме пунктирной стрелкой и являющееся по сути координатным выражением скалярного произведения векторов. Найдем формулу этого координатного выражения.

Пусть 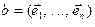‑ базис 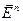, 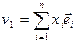и 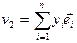‑ векторы из 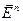. Тогда для скалярного произведения получаем

,

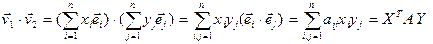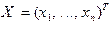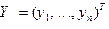где и ‑ координатные столбцы векторов и 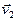соответственно, а матрица 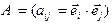называется матрица скалярного произведения в базисе 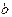. Таким образом .

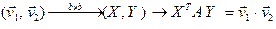Упражнение 0.1.

1). Отображение, где ­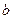‑ ортонормированный базис, сохраняет структуру евклидова векторного пространства, то есть

а). Отображение переводит сумму векторов в сумму векторов, а произведение вектора на число в произведение вектора на число (сохранение структуры векторного пространства).

б). Отображение сохраняет скалярное произведение:

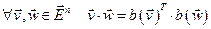
В левой части (Л.Ч) равенства точка означает скалярное произведение, а в П.Ч. – стандартное скалярное произведение в 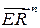, то есть обычное умножение строки на столбец.

2). Отображение сохраняет структуру аффинного пространства, то есть переводит отображение Вейля в отображение Вейля. Об этом и говорит равенство.