Теорема. Если функция  строго монотонна на интервале
строго монотонна на интервале 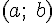 и имеет ненулевую производную
и имеет ненулевую производную 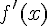 в произвольной точке этого интервала, то обратная ей функция
в произвольной точке этого интервала, то обратная ей функция 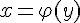 также имеет производную
также имеет производную 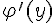 , в соответствующей точке, определяемую равенством
, в соответствующей точке, определяемую равенством 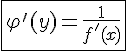
или 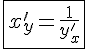 .
.
Пример. Рассмотрим функцию 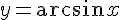 . Найдем ее производную.
. Найдем ее производную.
Решение. Пользуясь правилом дифференцирования обратной функции, найдем производную 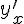 . Функция, обратная к исходной, имеет вид:
. Функция, обратная к исходной, имеет вид: 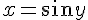 . Находим производную обратной функции:
. Находим производную обратной функции: 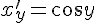 . Следовательно,
. Следовательно,
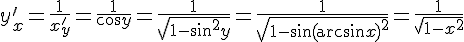
Получили, что 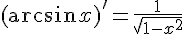 .
.
Вопрос. Дана функция 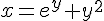 . Производная
. Производная 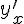 равна
равна
Начало формы
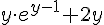 | |
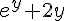 | |
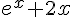 | |
1/ey+2y
Конец формы
Дифференцируемость функции.
Связь между непрерывностью и дифференцируемостью функции
Пусть функция  имеет в точке
имеет в точке 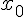 отличную от нуля производную, то есть
отличную от нуля производную, то есть
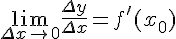 .
.
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
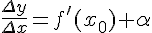 , где
, где  при
при 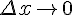 ,
,
или 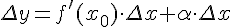 .
.
Таким образом, приращение функции 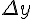 представляет собой сумму двух слагаемых
представляет собой сумму двух слагаемых 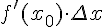 и
и 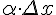 , которые являются бесконечно малыми функциями при
, которые являются бесконечно малыми функциями при 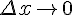 . При этом первое слагаемое есть бесконечно малая функция одного порядка с
. При этом первое слагаемое есть бесконечно малая функция одного порядка с 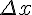 , а второе слагаемое есть бесконечно малая более высокого порядка, чем
, а второе слагаемое есть бесконечно малая более высокого порядка, чем 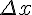 . Поэтому первое слагаемое
. Поэтому первое слагаемое 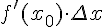 называется главной частью приращения функции
называется главной частью приращения функции  или дифференциалом функции
или дифференциалом функции  в точке
в точке 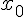 .
.
Определение 1. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 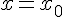 , если её приращение
, если её приращение 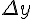 в этой точке можно представить в виде:
в этой точке можно представить в виде:
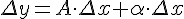
где 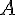 некоторое число, не зависящее от
некоторое число, не зависящее от 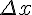 , причем
, причем 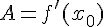 , а
, а  при
при 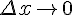 , то есть
, то есть 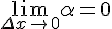 .
.
Понятия дифференцируемости функции в точке и существования производной в этой же точке тесно связаны между собой. Для функции одной переменной эти понятия являются равносильными.
Теорема 1. Для того чтобы функция  , была дифференцируема в точке
, была дифференцируема в точке 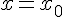 , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Определение 2. Функция  называется дифференцируемой на отрезке
называется дифференцируемой на отрезке 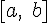 , если она дифференцируема в каждой точке этого отрезка.
, если она дифференцируема в каждой точке этого отрезка.
Теорема 2. Если функция  дифференцируема в некоторой точке
дифференцируема в некоторой точке 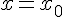 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Обратное утверждение неверно. Функция может быть непрерывной в точке, но не быть дифференцируемой, то есть не иметь конечной производной в этой точке.
В точках разрыва (точках, в которых функция не является непрерывной) функция не может иметь производную, поэтому в таких точках функция не дифференцируема.
Пример 1. Функция 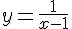 имеет точку разрыва
имеет точку разрыва 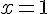 , следовательно, в этой точке она не дифференцируема.
, следовательно, в этой точке она не дифференцируема.
Пример 2. Функция 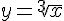 не имеет точек разрыва, но в точке
не имеет точек разрыва, но в точке 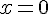 не имеет конечной производной, так как
не имеет конечной производной, так как
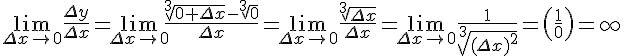 .
.
Следовательно, в точке 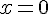 функция
функция 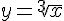 является непрерывной, но не дифференцируемой.
является непрерывной, но не дифференцируемой.
Вопрос. Какая из этих функций не дифференцируема в точке 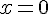 ?
?
Начало формы
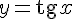 | |
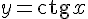 | |
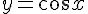 | |
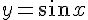 |
 2015-07-14
2015-07-14 9111
9111
