Пусть функция  дифференцируема в точке
дифференцируема в точке 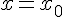 , то есть ее приращение можно записать в виде:
, то есть ее приращение можно записать в виде:
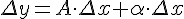 , где
, где  при
при 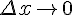 ,
, 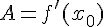 .
.
Первое слагаемое 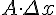 линейно относительно
линейно относительно 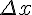 и является главной частью приращения функции
и является главной частью приращения функции  .
.
Определение. Дифференциалом функции  в точке
в точке 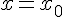 называется главная, линейная относительно
называется главная, линейная относительно 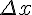 часть приращения функции
часть приращения функции 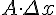 и обозначается
и обозначается 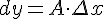 или
или 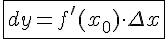 (читается "дэ игрек").
(читается "дэ игрек").
Дифференциалом независимой переменной 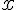 называется приращение этой переменной
называется приращение этой переменной 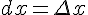 . Поэтому дифференциал функции
. Поэтому дифференциал функции  равен:
равен:
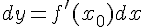 . Таким образом,
. Таким образом, 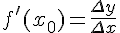 .
.
Пример. Вычислите дифференциал функции 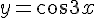 .
.
Решение. Так как дифференциал функции равен произведению производной этой функции на дифференциал аргумента, то 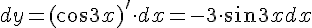 .
.
Инвариантность формы первого дифференциала
Пусть даны две дифференцируемые функции 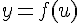 и
и 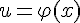 , образующие сложную функцию
, образующие сложную функцию 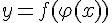 . По теореме о производной сложной функции можно написать:
. По теореме о производной сложной функции можно написать:
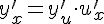
Умножив обе части этого равенства на 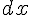 , получаем:
, получаем:
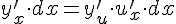 .
.
Но 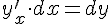 и
и 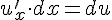 . Следовательно,
. Следовательно, 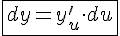 .
.
Таким образом, первый дифференциал функции  определяется одной и той же формулой независимо от того, является ли её аргумент независимой переменной или является функцией другого аргумента.
определяется одной и той же формулой независимо от того, является ли её аргумент независимой переменной или является функцией другого аргумента.
Это свойство дифференциала называется инвариантностью (неизменностью) формы первого дифференциала.
Вопрос. Дифференциал 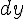 функции
функции 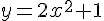 равен:
равен:
Начало формы
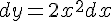 | |
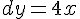 dy=4x dy=4x | |
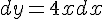 | |
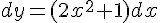 | |
 2015-07-14
2015-07-14 2561
2561
