Геометрический смысл дифференциала функции

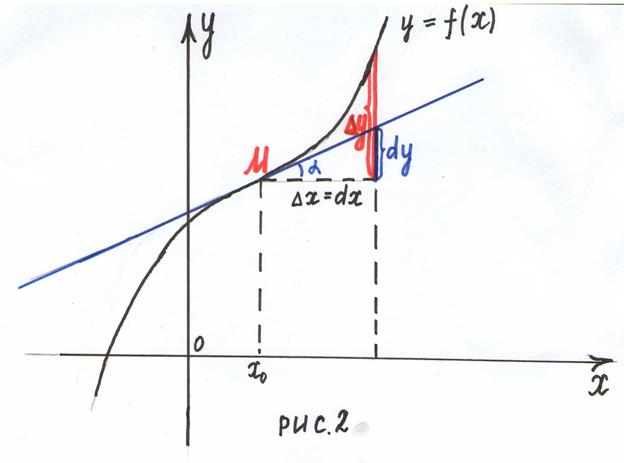
Дифференциал функции имеет следующий геометрический смысл. Дифференциал функции 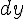в точке 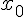равен приращению ординаты касательной к графику этой функции в точке 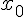, если приращение аргумента есть величина .

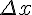Приращение функции 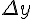есть приращение самой функции в точке 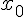при таком же приращении аргумента 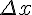. (рис.2)

Пример. Найти дифференциал 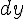и приращение 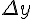функции 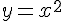в точке 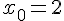, если приращение аргумента есть .

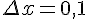Решение. Приращение функции равно: .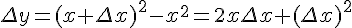

Дифференциал функции равен: .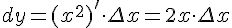

Есл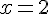и и 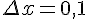то получим:

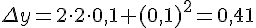и .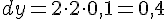

Ответ: .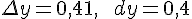

Вопрос. Разность 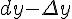между дифференциалом и приращением для функции 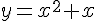в точке 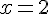при 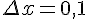равна

Начало формы

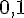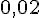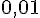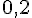Конец формы