Приведем основные формулы, которые используются в приближенных вычислениях с помощью дифференциала.
Если функция 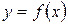 дифференцируема в точке х 0, то её приращение
дифференцируема в точке х 0, то её приращение 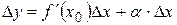 , где
, где 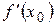 - производная функции в точке х 0, ∆ х – приращение аргумента,
- производная функции в точке х 0, ∆ х – приращение аргумента, 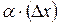 - бесконечно малая величина более высокого порядка чем ∆ х
- бесконечно малая величина более высокого порядка чем ∆ х 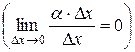 .
.
Отсюда следует приближенное равенство 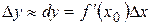 или
или 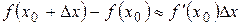 .
.
Следовательно, справедливо приближенное равенство
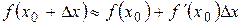 . (2.1)
. (2.1)
Данное равенство тем точнее, чем меньше ∆ х.
Пример 1. Вычислить приближенно Cos 91°.
Решение
Рассмотрим функцию 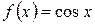 , найдем
, найдем 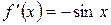 .
.
Согласно равенству (2.1), 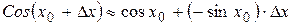 .
.
Учитывая, что 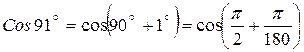 , возьмем
, возьмем
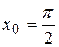 и
и 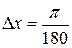 .
.
Тогда имеем конечный результат: 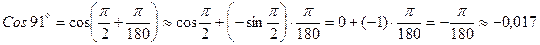 .
.
Пример 2. Вычислить приближенно 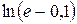 .
.
Решение
Рассмотрим функцию 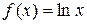 , найдем
, найдем 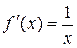 .
.
Согласно равенству (2.1), 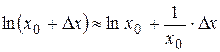 . За х 0 возьмем е, за ∆ х – (-0,1), тогда
. За х 0 возьмем е, за ∆ х – (-0,1), тогда
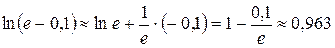 .
.
Пример 3. В результате наблюдений было установлено, что размер вклада клиента Сидорова в банке изменяется по закону 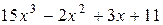 , где х – время в месяцах. Найти приблизительно размер вклада через 3,008 месяца.
, где х – время в месяцах. Найти приблизительно размер вклада через 3,008 месяца.
Решение
Воспользуемся приближенной формулой
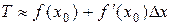 ,
,
где Т – вклад; х 0 = 3; ∆ х = 0,008; 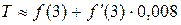 ;
; 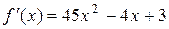 .
.
Тогда размер вклада примерно равен:
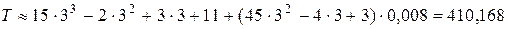 .
.
 2015-07-14
2015-07-14 4794
4794
