2015-07-14
2733
При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего значений функции на промежутке Х.
Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:
1. Найти производную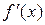 
.
2. Найти критические точки функции, в которых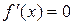 
или не существует.
3. Найти значения функции в критических точках, входящих в отрезок, а также на концах заданного отрезка и выбрать из них наибольшее f наиб = М и наименьшее f наим = m.
Пример 1. Найти наибольшее и наименьшее значения функции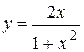 
на отрезке [0;2].
Решение
1. 
.
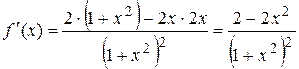2. 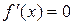, откуда критические точки х 1 = 1; х 2 = -1.
3. Критическая точка х 2 = -1 не принадлежит [0;2]. Значения функции в критических точках и на концах отрезка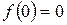 
, 
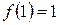и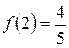 
.
Итак,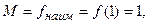 
.
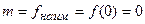Для решения текстовой задачи на нахождение наибольшего (наименьшего) значения функции следует исходя из её условия: выбрать независимую переменную, установить границы ее изменения (промежуток изменения) и выразить исследуемую величину через эту переменную как функцию. Затем проводится исследование этой функции на экстремум и по известному правилу находится наибольшее (наименьшее) значение. Результат анализируется на основании данных задачи.
Пример 2. Капитал в 1 млрд руб. может быть размещен в банке под 50% годовых или инвестирован в производство, причем эффективность вложения в производство ожидается в размере 100%, а издержки задаются квадратичной зависимостью. Прибыль облагается налогом в р %. При каких значениях р вложение в производство является более эффективным, нежели чистое размещение капитала под проценты в банке?
Решение. Пусть х (млрд руб.) инвестируется в производство, тогда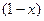 
- размещаются под проценты в банк. Размещенный капитал через год станет равным 
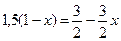, а капитал, вложенный в производство, - 
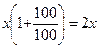. Издержки составят 
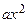, где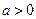 
.
Тогда прирост денежной массы от вложения в производство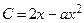 
. Так как налог на прирост равен 
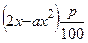, то прибыль от вложения в производство 
.
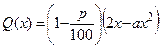Общая сумма прибыли через год определяется функцией
.
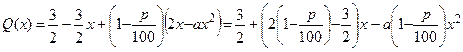Найдем максимальное значение этой функции на отрезке [0;1].
Вычислим производную:
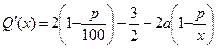х.
Приравняем ее к нулю и найдем значение х:
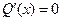при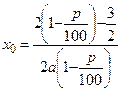 
.
Так как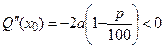 
, то х 0 – точка максимума.
Теперь найдем значение р, если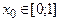 
. Решив неравенство 
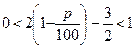, получим р <25.
Таким образом, если р >25, то выгоднее ничего не вкладывать в производство и разместить весь капитал в банк. Если р <25, то прибыль А больше, если деньги будут инвестированы в производство.
Пример 3. По прямой АВ (см. рис.4) проходит железнодорожный путь. В стороне на расстоянии s от пути находится пункт С, из которого следует перевести груз в пункт А. Предположим, что из пункта С можно добраться по прямой до произвольной точки железной дороги.
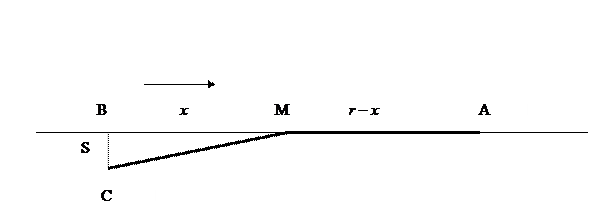
Рис. 4
По какой трассе следует перевезти груз из пункта С до железной дороги, а затем по железной дороге до пункта А, чтобы транспортные расходы были минимальными, если известно, что издержки по перевозке 1 тонны груза автотранспортом в 3 раза выше, чем издержки при перевозке по железной дороге на такое же расстояние, а также если транспортные расходы пропорциональны расстоянию? Вычислить минимальные транспортные издержки по полученной трассе.
Решение
Проведем [CB]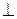 
[BA]. Пусть |ВА| = r. Предположим, что мы перевозим груз автотранспортом от С до М – какого-либо пункта на железной дороге. Введем обозначение |ВМ| = х.
Если груз необходимо перевезти по железной дороге на расстояние r от пункта В, то путь по железной дороге составит r-x. Так как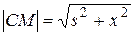 
, транспортные расходы составляют:
, 
.
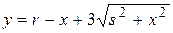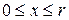Найдем, при каком значении х транспортные расходы будут минимальными. Для этого найдем наименьшее значение полученной выше функции на отрезке [0;r].
.
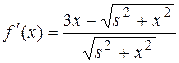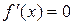, откуда критические точки 
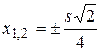, но из этих точек лишь 
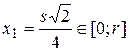, поэтому экстремум функции может быть только при 
.
; 
,
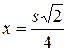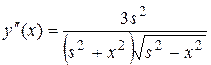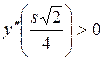т.е. при 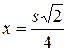функция транспортных расходов имеет минимум. Найдем его 
.
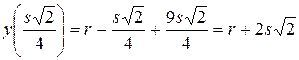Следовательно, транспортные расходы минимальны, если груз перевозят на автотранспорте до пункта М, расположенного на расстоянии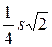 
от пункта В.
